What Percent Of 100 Is 4
Kalali
Apr 09, 2025 · 5 min read
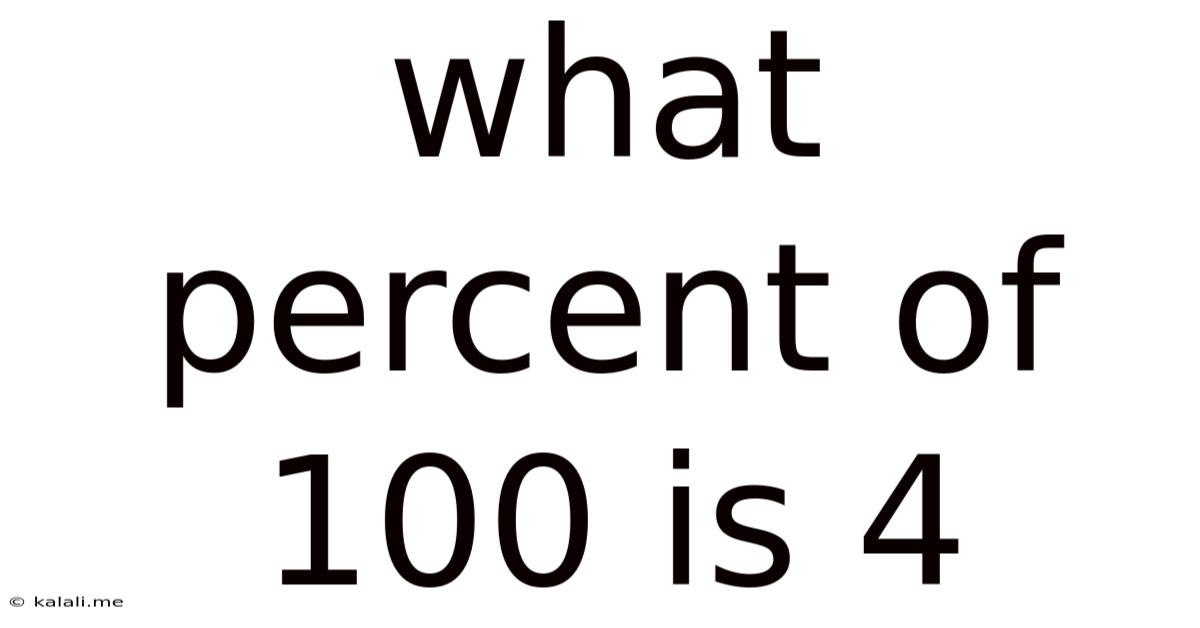
Table of Contents
What Percent of 100 is 4? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What percent of 100 is 4?", opens the door to a broader understanding of percentages, their calculation, and their wide-ranging applications in various fields. While the answer itself is straightforward (4%), the process of arriving at it and the underlying concepts offer valuable insights into mathematical principles and their practical uses. This article will explore the solution, delve into the mechanics of percentage calculations, and examine real-world scenarios where understanding percentages is crucial.
Meta Description: Learn how to calculate percentages, understand the concept of "what percent of 100 is 4," and discover the practical applications of percentages in everyday life and various professions. This comprehensive guide provides step-by-step explanations and real-world examples.
Understanding Percentages: A Foundation
Before we tackle the specific problem, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 4% means 4 out of 100, or 4/100. This fundamental concept forms the basis for all percentage calculations.
Calculating "What Percent of 100 is 4?"
The question "What percent of 100 is 4?" can be solved using a simple proportion:
- Let x represent the unknown percentage.
- We can set up a proportion: x/100 = 4/100
- Solving for x: To solve this equation, we can cross-multiply: 100x = 400
- Dividing both sides by 100: x = 4
Therefore, 4 is 4% of 100.
This simple calculation demonstrates the core principle of percentage calculation: relating a part to a whole, expressed as a fraction of 100.
Beyond the Basics: Calculating Percentages with Different Whole Numbers
While the example using 100 as the whole number is straightforward, the concept applies equally to any whole number. Let's explore how to calculate percentages in more complex scenarios:
Scenario 1: Finding the percentage of a different whole number.
What percent of 250 is 50?
- Set up a proportion: x/100 = 50/250
- Cross-multiply: 250x = 5000
- Solve for x: x = 20
Therefore, 50 is 20% of 250.
Scenario 2: Finding a specific percentage of a number.
What is 15% of 300?
- Convert the percentage to a decimal: 15% = 0.15
- Multiply the decimal by the whole number: 0.15 * 300 = 45
Therefore, 15% of 300 is 45.
Scenario 3: Finding the original whole number when given a percentage and its value.
12 is 20% of what number?
- Set up a proportion: 12/x = 20/100
- Cross-multiply: 1200 = 20x
- Solve for x: x = 60
Therefore, 12 is 20% of 60.
These examples illustrate the versatility of percentage calculations and demonstrate the importance of understanding the underlying principles.
Practical Applications of Percentages: Real-world Examples
Percentages are ubiquitous in everyday life, influencing decisions and shaping our understanding of various aspects of the world around us. Here are some prominent examples:
-
Finance: Interest rates on loans and savings accounts, discount percentages in sales, tax calculations, investment returns, and profit margins are all expressed as percentages. Understanding these percentages is crucial for making informed financial decisions. For example, understanding a 5% interest rate on a loan helps you calculate the total cost of borrowing. Similarly, recognizing a 20% discount on a purchase allows for quick calculation of savings.
-
Science and Statistics: Percentages are used to represent data in scientific research and statistical analysis. For example, researchers might report the percentage of participants who responded positively to a treatment, or the percentage change in a particular variable over time. This allows for a clear representation of trends and outcomes in an easily understandable format.
-
Retail and Marketing: Discounts, sales tax, markups, and profit margins are all expressed using percentages. Retail businesses use percentages to manage their pricing strategies and track profitability. Marketing campaigns often rely on percentage-based metrics to measure their effectiveness, such as conversion rates and click-through rates.
-
Healthcare: Healthcare professionals use percentages to express various health statistics, such as the percentage of the population vaccinated against a particular disease, or the percentage change in a patient's blood pressure. These vital metrics provide insights into public health trends and individual patient progress.
-
Education: Grade percentages, test scores, and class participation rates are frequently expressed as percentages to provide a clear and quantifiable measure of student performance. Teachers utilize percentage calculations to determine final grades and track student progress.
-
Everyday Life: Many everyday tasks involve percentage calculations. Calculating tips at restaurants, figuring out sales tax on purchases, or understanding nutritional information on food labels all require an understanding of percentages.
Advanced Percentage Calculations and Concepts
Beyond the basic calculations, understanding more complex percentage concepts can provide a deeper understanding of mathematical principles and their real-world application. This includes:
-
Percentage Increase and Decrease: These calculations determine the change in a quantity expressed as a percentage. The formula for percentage increase is [(New Value - Old Value) / Old Value] * 100, and for percentage decrease, it's [(Old Value - New Value) / Old Value] * 100. Understanding these formulas is critical in tracking changes in various data sets, such as population growth or economic indicators.
-
Compound Interest: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. Understanding this concept is crucial for long-term financial planning and investment strategies.
-
Percentage Points: Percentage points represent the absolute difference between two percentages, not the relative change. For example, an increase from 10% to 15% is a 5-percentage point increase, but a 50% relative increase. Differentiating between these concepts is crucial for accurate interpretation of data.
-
Weighted Averages: These are averages where certain values are given more importance than others. They’re frequently used in calculating GPA, indices, or composite scores, which might weight different elements differently.
Conclusion: Mastering Percentages for a Quantified World
The question "What percent of 100 is 4?" serves as a gateway to a much wider understanding of percentages and their applications. From everyday calculations to complex financial models, the ability to work comfortably with percentages is an invaluable skill. Mastering these concepts provides a powerful tool for navigating a world increasingly defined by quantitative data and informed decision-making. Understanding not only the basic calculations but also the more advanced concepts will significantly enhance one's ability to interpret data, analyze trends, and make sound judgements across various aspects of life. This detailed exploration should empower readers to confidently tackle percentage-related problems and apply this knowledge effectively in their professional and personal endeavors.
Latest Posts
Latest Posts
-
Flowering Plants Separated Into Different Classifications
Apr 17, 2025
-
How Much Is 33 Inches In Feet
Apr 17, 2025
-
What Is 205 Celsius In Fahrenheit
Apr 17, 2025
-
71 Inches Is How Many Cm
Apr 17, 2025
-
13 3 As A Mixed Number
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 100 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.