What Percent Of 15 Is 20
Kalali
Mar 08, 2025 · 5 min read
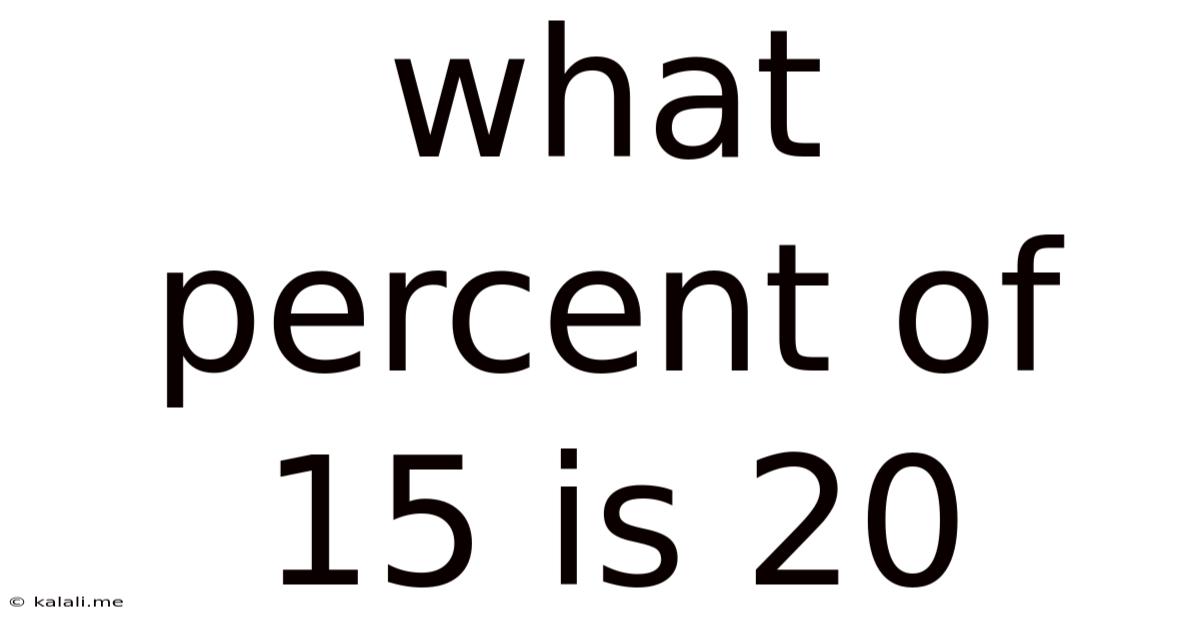
Table of Contents
What Percent of 15 is 20? Understanding Percentages and Their Applications
This seemingly simple question, "What percent of 15 is 20?", opens a door to a vast world of mathematical concepts and their real-world applications. It's more than just a basic percentage problem; it's a gateway to understanding ratios, proportions, and how percentages are used in various fields, from finance and statistics to everyday life. This article will delve deep into solving this problem, exploring the underlying principles, and demonstrating its relevance in practical scenarios.
Understanding Percentages
Before we tackle the specific problem, let's establish a firm grasp of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5. Understanding this basic definition is crucial for solving percentage problems.
Solving "What Percent of 15 is 20?"
The question "What percent of 15 is 20?" asks us to find the percentage that, when applied to 15, results in 20. This is a classic percentage problem that can be solved using several methods.
Method 1: Using Proportions
One common method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
x/100 = 20/15
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
15x = 2000
Then, divide both sides by 15:
x = 2000/15 = 133.33 (approximately)
Therefore, 20 is approximately 133.33% of 15.
Method 2: Using Decimal Conversion
Another approach involves converting the fraction 20/15 into a decimal and then multiplying by 100 to express it as a percentage.
20/15 = 1.3333...
Multiplying by 100 gives:
1.3333... * 100 = 133.33%
This confirms our result from the proportion method.
Understanding the Result: A Percentage Greater Than 100%
The result, 133.33%, might seem counterintuitive at first glance. It's important to remember that percentages can be greater than 100%. A percentage greater than 100% simply means that the resulting value (20) is larger than the original value (15). This indicates an increase or growth.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in various real-world scenarios. Here are a few examples:
1. Finance and Investments:
- Calculating returns: Investors frequently calculate percentage returns on their investments. If an investment of $15,000 grows to $20,000, the percentage increase is 133.33%, indicating substantial growth.
- Interest calculations: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations is crucial for managing personal finances effectively.
- Analyzing financial statements: Financial analysts use percentages to analyze financial statements, such as income statements and balance sheets, to assess the financial health of a company. Key ratios like profit margins and return on equity are expressed as percentages.
2. Statistics and Data Analysis:
- Calculating percentages in surveys and polls: Survey data is often presented in percentages. For example, a survey might reveal that 20% of respondents prefer a particular product.
- Representing proportions in data sets: Percentages provide a convenient way to summarize and compare proportions within larger datasets. This is crucial for understanding trends and patterns.
- Calculating growth rates: In economics and demographics, percentage changes are used to measure growth rates of various variables like GDP, population, and inflation.
3. Everyday Life:
- Calculating discounts and sales tax: Stores use percentages to advertise discounts ("20% off!") and to calculate sales tax on purchases.
- Calculating tips and gratuities: People often calculate tips as a percentage of the bill amount (e.g., a 15% tip).
- Determining proportions in recipes: Recipes often include percentages to indicate the proportion of different ingredients.
Expanding the Understanding: Beyond the Basic Calculation
While the core problem focuses on finding what percentage of 15 is 20, exploring related concepts enhances our understanding of percentages.
1. Finding a Percentage of a Number:
This is the inverse of the problem we solved. If we wanted to find 133.33% of 15, we would multiply 15 by 1.3333, resulting in 20. This shows the relationship between the percentage and the resulting value.
2. Percentage Change:
A closely related concept is percentage change, which measures the relative change between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100
In our case, the percentage change from 15 to 20 is:
[(20 - 15) / 15] * 100 = 33.33%
This indicates a 33.33% increase from 15 to 20.
3. Applications in Various Fields:
The use of percentages extends far beyond simple calculations. Understanding percentages is crucial in fields like:
- Engineering: Engineers use percentages to represent tolerances, efficiency, and error rates.
- Healthcare: Percentages are used to express disease prevalence, treatment success rates, and risk factors.
- Science: In various scientific disciplines, percentages are used to represent concentrations, yields, and experimental results.
Conclusion: The Power of Percentages
The seemingly simple question, "What percent of 15 is 20?", reveals the fundamental importance of percentage calculations in diverse fields. Mastering percentage calculations allows for a deeper understanding of ratios, proportions, and data analysis. From managing personal finances to interpreting scientific data, the ability to calculate and interpret percentages is a vital skill in today's world. Beyond the basic calculation, understanding the underlying concepts and exploring related topics enhances the ability to apply this knowledge effectively in numerous real-world situations. The seemingly simple problem serves as a powerful illustration of the wide-reaching implications of a foundational mathematical concept.
Latest Posts
Latest Posts
-
Is Dried Oregano A Pure Substance Or Mixture
Jul 04, 2025
-
What Is Fgteev Duddys Real Phone Number
Jul 04, 2025
-
What Are 2004 Pennies Worth Worlds Easyest Game
Jul 04, 2025
-
Who Did Alan Jackson Have An Affair With
Jul 04, 2025
-
How Much Is 500 Grams Of Ground Beef
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.