What Percent Of 15 Is 3
Kalali
Apr 04, 2025 · 5 min read
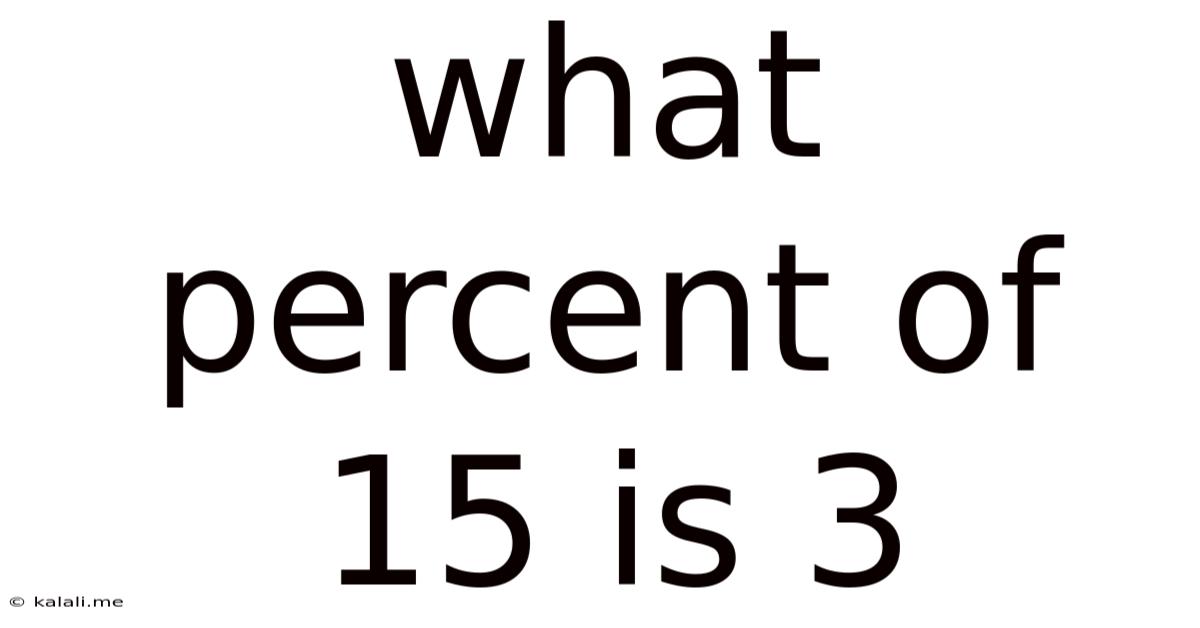
Table of Contents
What Percent of 15 is 3? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and sales tax to understanding financial reports and statistical data. This comprehensive guide will not only answer the question "What percent of 15 is 3?" but also delve into the underlying principles of percentage calculations, providing you with the tools to solve similar problems with ease.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" or "out of 100". We use the symbol "%" to represent percentages. For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Solving "What Percent of 15 is 3?"
The question "What percent of 15 is 3?" can be solved using several methods. Let's explore the most common and effective approaches.
Method 1: Using the Proportion Method
This method relies on setting up a proportion, which is an equation stating that two ratios are equal. We can represent the problem as:
- x/100 = 3/15
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
- 15x = 300
Then, divide both sides by 15:
- x = 20
Therefore, 3 is 20% of 15.
Method 2: Using the Decimal Method
This method involves converting the fraction 3/15 into a decimal and then multiplying by 100 to express it as a percentage.
- Convert the fraction to a decimal: 3 divided by 15 equals 0.2
- Multiply the decimal by 100: 0.2 * 100 = 20
Therefore, 3 is 20% of 15.
Method 3: Using the Formula Method
The percentage formula provides a direct way to calculate percentages:
- Percentage = (Part / Whole) * 100
In this case:
- Part = 3
- Whole = 15
Substituting these values into the formula:
- Percentage = (3 / 15) * 100 = 0.2 * 100 = 20%
Again, we find that 3 is 20% of 15.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
1. Discounts and Sales Tax
Retail stores frequently advertise discounts as percentages. For example, a 20% discount on a $50 item means you'll save 20% of $50, which is $10. Similarly, sales tax is often calculated as a percentage of the purchase price.
2. Financial Analysis
Percentage changes are widely used in financial reporting to track growth or decline in various metrics like revenue, profits, and stock prices. For example, if a company's revenue increases from $100 million to $120 million, the percentage increase is calculated as ((120-100)/100)*100 = 20%.
3. Grades and Test Scores
School grades are often expressed as percentages, representing the proportion of correctly answered questions or the overall performance in a subject. For instance, a score of 85% on a test indicates that 85 out of 100 possible points were obtained.
4. Statistical Data Interpretation
Percentages play a crucial role in interpreting statistical data. For example, survey results are frequently presented as percentages to show the proportion of respondents holding a particular opinion or exhibiting a specific characteristic.
Advanced Percentage Calculations
Beyond the basic percentage calculations, several more advanced concepts exist, such as:
1. Percentage Increase/Decrease
Calculating percentage change involves determining the difference between two values and expressing it as a percentage of the original value. The formula is:
- Percentage Change = [(New Value - Old Value) / Old Value] * 100
A positive percentage change indicates an increase, while a negative percentage change indicates a decrease.
2. Percentage Point Difference
This term is often misused, leading to confusion. A percentage point difference represents the actual difference between two percentages. For example, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points (8% - 5% = 3 percentage points), not 60%.
3. Compound Percentage Growth
This concept applies when a percentage increase or decrease is applied repeatedly over time. For instance, if an investment grows by 10% each year for three years, the final value will be significantly higher than simply multiplying the initial value by 30%. Compound interest calculations utilize this concept.
Troubleshooting Common Percentage Calculation Mistakes
Several common mistakes can arise when working with percentages:
-
Confusing Percentage Change with Percentage Points: As mentioned earlier, this is a frequent error. Remember to distinguish between the absolute difference and the relative change.
-
Incorrectly Applying the Formula: Double-check the formula to ensure you're correctly identifying the 'part' and the 'whole' in your calculations.
-
Not Converting to Decimal: When using the formula or performing calculations, remember that percentages must often be converted to their decimal equivalents (e.g., 20% becomes 0.20).
-
Rounding Errors: Rounding numbers too early in calculations can lead to accumulated errors in the final result. Aim to round only the final answer to the desired level of precision.
Practical Tips for Mastering Percentages
-
Practice Regularly: The key to mastering any mathematical concept, including percentages, is consistent practice. Solve various percentage problems to build your confidence and understanding.
-
Use Different Methods: Experiment with different calculation methods (proportion, decimal, formula) to find the approach that suits your learning style best.
-
Check Your Work: Always double-check your answers to ensure accuracy. Use a calculator or alternate methods to verify your results.
-
Break Down Complex Problems: When dealing with intricate percentage problems, break them down into smaller, more manageable steps.
Conclusion
This comprehensive guide has not only answered the question "What percent of 15 is 3?" (which is 20%) but also provided a solid foundation in understanding and applying percentage calculations. Remember, percentages are a fundamental tool used across various fields, and mastering them will significantly enhance your problem-solving abilities in daily life and professional settings. By understanding the methods discussed and practicing regularly, you can confidently tackle any percentage calculation that comes your way. Keep practicing, and you'll soon become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Cuanto Es 48 Pulgadas En Metros
Apr 10, 2025
-
112 Minutes Is How Many Hours
Apr 10, 2025
-
How Many Inches In 22 5 Cm
Apr 10, 2025
-
How Much Water Is 120 Oz
Apr 10, 2025
-
Cuanto Es 1 80 Metros En Pies
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.