What Percent Of 16 Is 3
Kalali
Apr 03, 2025 · 5 min read
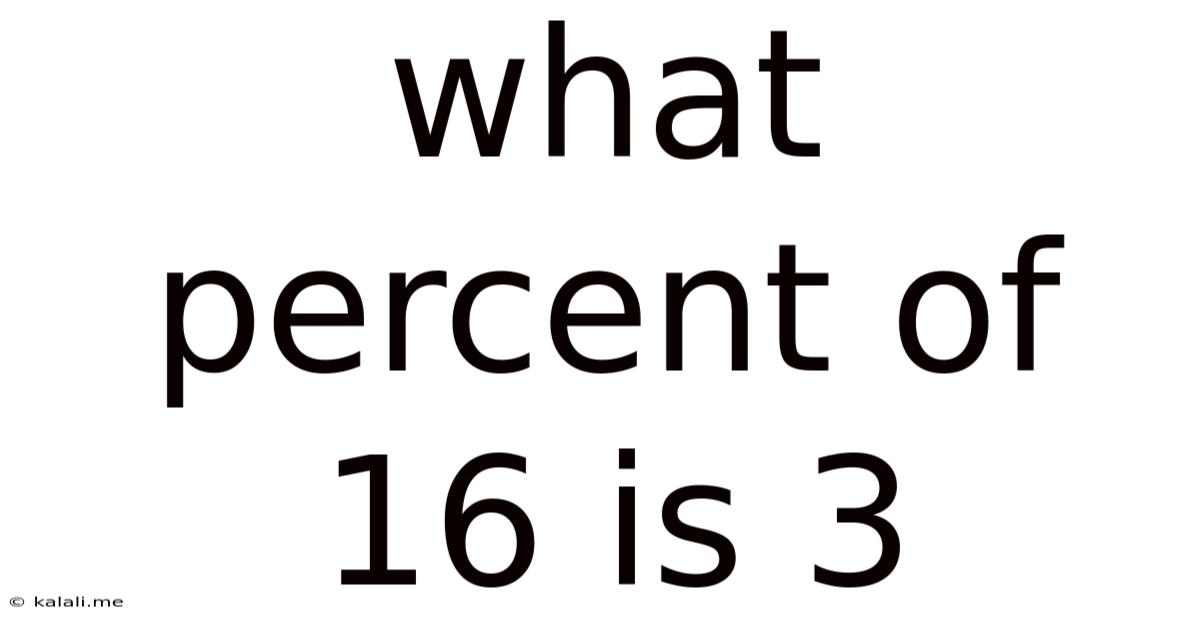
Table of Contents
What Percent of 16 is 3? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 16 is 3?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for anyone wanting to master percentages and apply them confidently in various situations. This article will delve into the solution, explore different approaches, and showcase the broader significance of percentage calculations.
Understanding Percentages: The Foundation
Before tackling the specific problem, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
This fundamental concept is vital because percentages allow us to easily compare proportions and make sense of data across various scales. Whether you're dealing with financial reports, scientific data, or everyday shopping, the ability to understand and calculate percentages is invaluable.
Method 1: Setting up the Proportion
The most common and intuitive method to solve "What percent of 16 is 3?" is by setting up a proportion. A proportion is an equation that states two ratios are equal. We can express the problem as follows:
- x/100 = 3/16
Where:
- 'x' represents the unknown percentage we are trying to find.
- '3' is the part (the number we're comparing).
- '16' is the whole (the total amount).
To solve for 'x,' we cross-multiply:
- 16x = 300
Then, divide both sides by 16:
- x = 300/16 = 18.75
Therefore, 3 is 18.75% of 16.
Method 2: Using the Percentage Formula
Another way to approach the problem is to utilize the standard percentage formula:
- Percentage = (Part / Whole) * 100
In our case:
- Percentage = (3 / 16) * 100
Performing the calculation:
- Percentage = 0.1875 * 100 = 18.75%
This method directly applies the definition of percentage, calculating the ratio of the part to the whole and then multiplying by 100 to express it as a percentage.
Method 3: Decimal Conversion and Multiplication
This approach involves converting the fraction 3/16 into a decimal first and then multiplying by 100 to express it as a percentage.
-
Convert the fraction to a decimal: 3 divided by 16 equals 0.1875.
-
Multiply by 100 to convert to a percentage: 0.1875 * 100 = 18.75%
This method demonstrates the direct relationship between decimals and percentages. Every decimal can be converted to a percentage by multiplying by 100, and vice versa.
Real-World Applications of Percentage Calculations
The ability to calculate percentages isn't just a mathematical exercise; it's a crucial life skill with widespread applications:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is essential for making informed financial decisions.
-
Science: Scientists frequently use percentages to represent data, such as the percentage of a population exhibiting a certain trait or the percentage change in a measured variable over time.
-
Retail: Discounts, sales tax, and markup percentages are fundamental to the retail industry. Consumers need to understand percentages to make informed purchasing decisions.
-
Statistics: Percentages are widely used in statistics to summarize and interpret data, allowing for easier comparison and analysis of different groups or datasets.
-
Everyday Life: Calculating tips at restaurants, understanding sale prices, and determining the percentage of a task completed are common scenarios where percentage knowledge is useful.
Beyond the Basics: More Complex Percentage Problems
While the "What percent of 16 is 3?" problem is relatively simple, the principles involved can be extended to more complex scenarios. For example:
-
Finding the whole: If you know a percentage and the part, you can calculate the whole using a modified version of the percentage formula.
-
Finding the part: If you know the percentage and the whole, you can calculate the part.
-
Percentage increase/decrease: Calculating percentage changes requires understanding how to determine the difference between two values and expressing that difference as a percentage of the original value.
These more advanced problems build upon the fundamental concepts explored in this article, demonstrating the versatility and importance of mastering percentage calculations.
Mastering Percentages: Tips and Practice
Developing proficiency in percentage calculations requires practice and a clear understanding of the underlying principles. Here are some tips:
-
Practice regularly: Work through various problems, starting with simple ones and gradually increasing the complexity.
-
Use different methods: Experiment with the various methods described in this article to find the approach that works best for you.
-
Understand the concepts: Don't just memorize formulas; understand the logic behind them. This will help you solve more complex problems and apply the concepts to real-world scenarios.
-
Use online resources: Numerous online calculators and tutorials can help you practice and reinforce your understanding of percentages.
-
Break down complex problems: If faced with a challenging problem, break it down into smaller, more manageable parts.
Conclusion: The Importance of Percentage Proficiency
The seemingly simple question, "What percent of 16 is 3?", provides a gateway to a broader understanding of percentage calculations and their widespread application. By mastering these calculations, you equip yourself with a valuable skill set applicable to diverse fields, from personal finance and shopping to scientific analysis and statistics. Regular practice and a focus on understanding the underlying principles will solidify your knowledge and allow you to confidently tackle more complex percentage problems in the future. The ability to accurately and efficiently calculate percentages is a cornerstone of numerical literacy, crucial for navigating the complexities of modern life.
Latest Posts
Latest Posts
-
What Is 68 Cm In Inches
Apr 04, 2025
-
166 Cm To Feet And Inches
Apr 04, 2025
-
1 1 2 Cup Of Water
Apr 04, 2025
-
How Much Is 10 Fl Oz
Apr 04, 2025
-
12 Ounces Of Water Is How Many Cups
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
