What Percent Of 16 Is 4
Kalali
Apr 27, 2025 · 5 min read
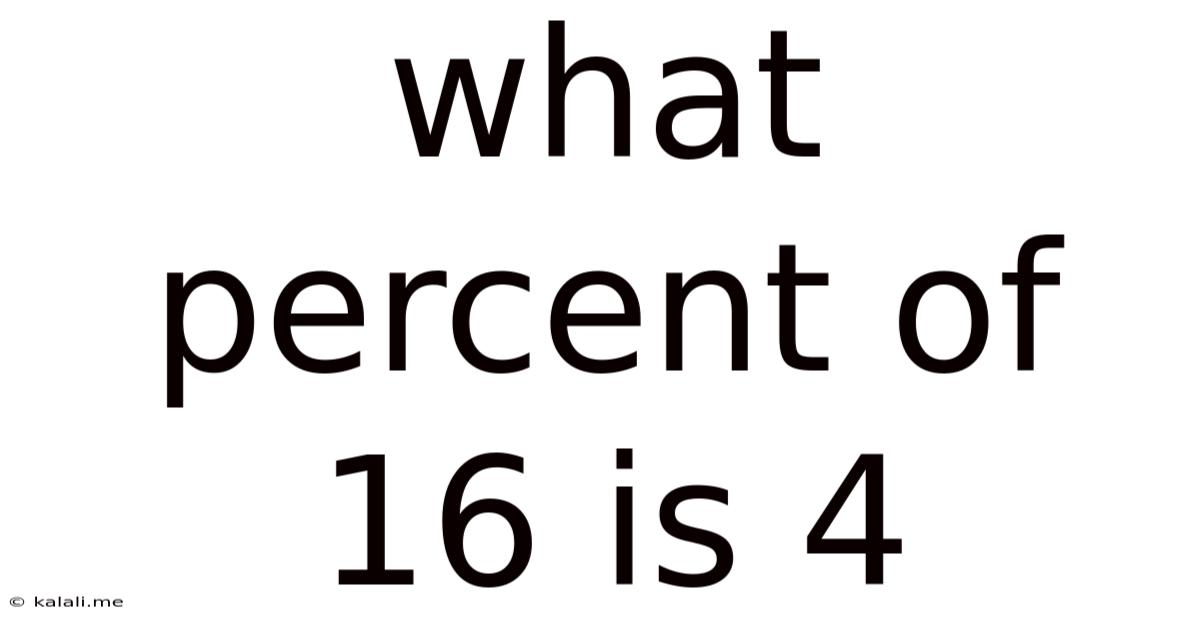
Table of Contents
What Percent of 16 is 4? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent of 16 is 4?" – opens the door to a broader understanding of percentages, their applications, and how to solve percentage problems with confidence. This article will not only answer the question directly but also explore the underlying mathematical concepts, different methods for solving similar problems, and real-world applications of percentage calculations.
Meta Description: Learn how to calculate percentages efficiently. This in-depth guide explains how to find what percent of 16 is 4, covering multiple methods, real-world applications, and advanced percentage concepts. Master percentage calculations with ease!
Understanding Percentages: The Basics
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per hundred." For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Percentages are used extensively in various fields, from finance and economics to statistics and everyday life. They provide a standardized way to compare proportions and represent parts of a whole. Understanding percentages is crucial for interpreting data, making informed decisions, and understanding concepts like interest rates, discounts, tax rates, and much more.
Method 1: Setting up a Proportion
One of the most common methods for solving percentage problems is by setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion:
x/100 = 4/16
Where 'x' represents the percentage we're trying to find. This proportion reads: "x out of 100 is equal to 4 out of 16."
To solve for 'x', we can cross-multiply:
16x = 4 * 100
16x = 400
x = 400 / 16
x = 25
Therefore, 4 is 25% of 16.
Method 2: Using the Percentage Formula
Another approach involves using the basic percentage formula:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 4
- Whole: 16
Substituting these values into the formula:
Percentage = (4 / 16) * 100
Percentage = 0.25 * 100
Percentage = 25
Again, we find that 4 is 25% of 16.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, we represent the relationship as a fraction: 4/16
Simplifying the fraction: 4/16 = 1/4
Converting the fraction to a decimal: 1/4 = 0.25
Finally, multiply by 100 to get the percentage: 0.25 * 100 = 25%
This confirms that 4 is indeed 25% of 16.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in many real-life situations. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $50, you can calculate the discount amount and the final price using percentage calculations.
-
Understanding Interest Rates: Banks and financial institutions use percentages to express interest rates on loans and savings accounts. Understanding percentages helps you make informed decisions about borrowing and saving money.
-
Analyzing Statistics: Percentages are frequently used to present statistical data, making it easier to understand and compare different proportions. For example, understanding the percentage change in a company's sales over a year or the percentage of people who voted for a certain candidate in an election.
-
Calculating Taxes: Sales tax, income tax, and property tax are all calculated using percentages. Understanding these calculations is crucial for managing personal finances effectively.
-
Determining Tips: When dining out, calculating a tip based on a percentage of the bill is a common practice.
-
Grading Systems: Many educational systems utilize percentages to represent student grades, making it easy to compare performance across different assessments.
-
Nutritional Information: Food labels often display nutritional information as percentages of recommended daily values, helping consumers make informed choices about their diet.
Solving More Complex Percentage Problems
While the problem "What percent of 16 is 4?" is relatively straightforward, the principles can be applied to more complex scenarios. Let's consider some variations:
-
Finding the Whole: If 25% of a number is 4, what is the number? In this case, you would set up the equation: 0.25x = 4, and solve for x.
-
Finding the Part: What is 30% of 80? Here, you would multiply 80 by 0.30.
-
Percentage Increase/Decrease: Calculate the percentage increase or decrease between two values. For instance, if a price increases from $10 to $12, the percentage increase is calculated as [(12-10)/10] * 100 = 20%.
Advanced Percentage Concepts
The understanding of basic percentage calculations can be further enhanced by exploring more advanced concepts such as:
-
Compound Interest: This concept deals with interest accumulating on both the principal amount and accumulated interest over time. It's crucial in understanding investments and loan repayments.
-
Percentage Points: It is important to differentiate between percentage change and percentage points. A change from 10% to 15% is a 5 percentage point increase but a 50% increase relative to the original 10%.
-
Weighted Averages: When dealing with different percentages associated with different weights, weighted averages are used to calculate an overall percentage. This is frequently applied in finance and statistics.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems accurately and efficiently is a valuable skill in many aspects of life. This article has provided a comprehensive overview of percentage calculations, from basic concepts to more complex applications. By mastering these methods and understanding the underlying principles, you'll be well-equipped to tackle various percentage-related challenges and make informed decisions in both personal and professional contexts. Remember that practice is key to solidifying your understanding and improving your speed and accuracy in solving these types of problems. Continuously working through various examples and applying these principles to real-world scenarios will enhance your proficiency in this essential mathematical skill. The seemingly simple question, "What percent of 16 is 4?", has indeed opened up a world of possibilities within the realm of percentage calculations.
Latest Posts
Latest Posts
-
4 1 4 As An Improper Fraction
Apr 28, 2025
-
Cuales Son Los Centimetros En Un Metro
Apr 28, 2025
-
How Much Is 170 Cm In Inches
Apr 28, 2025
-
What Was Darwin Influences On Lyell And Hutton
Apr 28, 2025
-
Convert 99 Degrees Fahrenheit To Celsius
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.