What Percent Of 16 Is 9
Kalali
Apr 24, 2025 · 5 min read
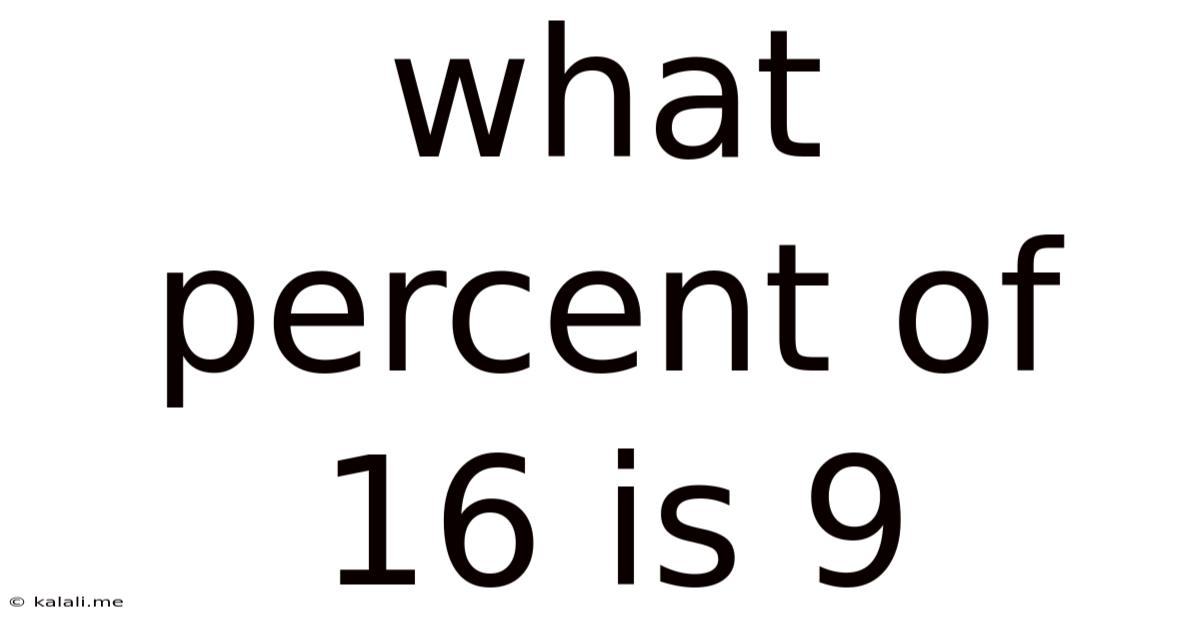
Table of Contents
What Percent of 16 is 9? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 16 is 9?", opens the door to a broader understanding of percentage calculations, their applications in everyday life, and the underlying mathematical principles. This article will not only answer the question directly but also explore the different methods for solving percentage problems, offering a comprehensive guide for anyone looking to improve their mathematical skills. Understanding percentages is crucial in various fields, from finance and budgeting to sales and statistics. Let's delve into the intricacies of this fundamental concept.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100." So, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5. Percentages are used to represent proportions, rates, and changes, making them a versatile tool for comparing and analyzing data.
Methods for Calculating Percentages
There are several approaches to solving percentage problems, and understanding each method can make you more versatile in tackling various scenarios. We'll explore the most common methods, including using proportions, equations, and the decimal method. Let's illustrate these using our example: "What percent of 16 is 9?"
1. The Proportion Method
This method uses the concept of ratios and proportions. We can set up a proportion to represent the problem:
- Part/Whole = Percentage/100
In our case:
- 9/16 = x/100
To solve for x (the percentage), we cross-multiply:
- 9 * 100 = 16 * x
- 900 = 16x
- x = 900/16
- x = 56.25
Therefore, 9 is 56.25% of 16.
2. The Equation Method
This method uses algebraic equations to solve for the unknown percentage. We can represent the problem as:
- x% * 16 = 9
To solve for x, we first convert the percentage to a decimal by dividing by 100:
- (x/100) * 16 = 9
Now, we can solve for x:
- 16x/100 = 9
- 16x = 900
- x = 900/16
- x = 56.25
Again, we find that 9 is 56.25% of 16.
3. The Decimal Method
This method involves converting the percentage to a decimal and then multiplying. First, we find what fraction 9 is of 16:
- 9/16 = 0.5625
Now, we convert this decimal to a percentage by multiplying by 100:
- 0.5625 * 100 = 56.25%
This confirms our previous results: 9 is 56.25% of 16.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. For instance, understanding the interest rate on a loan or the discount on a sale item requires proficiency in percentage computations. Understanding compound interest, which involves calculating interest on the principal plus accumulated interest, is critical for long-term financial planning.
-
Sales and Marketing: Businesses use percentages to track sales growth, conversion rates, and market share. Analyzing sales data using percentages helps businesses understand their performance and make informed decisions about marketing strategies. Calculating customer retention rates (percentage of customers who continue using a service) is crucial for long-term business sustainability.
-
Statistics: Percentages are fundamental in statistical analysis, allowing for the comparison of different data sets and the representation of proportions within a population. For example, understanding survey results often involves calculating percentages of respondents who chose particular options.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, and understanding tax rates are all common scenarios where percentage calculations are used.
Advanced Percentage Problems and Techniques
Beyond the basic calculations, there are more complex percentage problems to consider:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100.
-
Percentage of a Percentage: This involves calculating a percentage of a previously calculated percentage. For example, finding 10% of 20% of a number requires a multi-step calculation.
-
Finding the Original Value: Given a percentage and a final value after a percentage increase or decrease, it's possible to calculate the original value using reverse percentage calculations.
Expanding Your Understanding of Percentages
To further enhance your understanding and proficiency in percentage calculations:
-
Practice Regularly: Solving various percentage problems is the key to mastery. Start with simpler problems and gradually move towards more complex ones.
-
Use Multiple Methods: Trying different methods for solving the same problem will deepen your understanding and help you identify the most efficient approach for each scenario.
-
Real-World Applications: Try applying percentage calculations to real-life situations, such as calculating discounts on shopping trips or analyzing financial data.
-
Utilize Online Resources: Numerous online resources, including calculators and tutorials, can provide additional support and practice opportunities.
Conclusion
The question "What percent of 16 is 9?" serves as a springboard for exploring the world of percentage calculations. Mastering percentages is a valuable skill with wide-ranging applications in various aspects of life. By understanding the different methods for solving percentage problems and practicing regularly, you can build confidence and proficiency in this essential mathematical concept. Remember, the key is not just to find the answer (56.25%), but to grasp the underlying principles and apply them to solve a wide array of percentage-related problems. This understanding will empower you to analyze data, make informed decisions, and navigate various real-world scenarios with greater ease and confidence.
Latest Posts
Latest Posts
-
How Many Milliliters Is 1 5 Liters
Apr 24, 2025
-
30 Ounces Is How Many Liters
Apr 24, 2025
-
How To Find The Range Of A Dot Plot
Apr 24, 2025
-
What Is 10 To The 12th Power
Apr 24, 2025
-
How Many Mm Is 1 1 4 Inch
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.