What Percent Of 2 Is 8
Kalali
Apr 09, 2025 · 5 min read
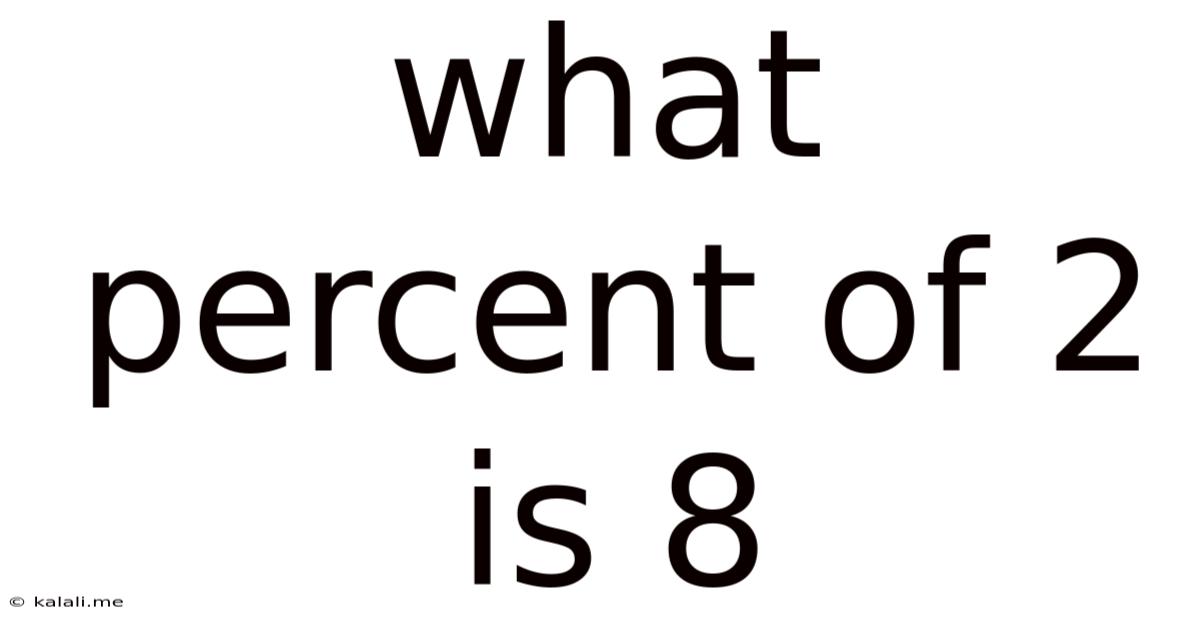
Table of Contents
What Percent of 2 is 8? Unpacking the Concept and Solving Percentage Problems
This seemingly simple question, "What percent of 2 is 8?", actually unlocks a fundamental understanding of percentages and their application in various mathematical contexts. It's a question that, at first glance, might seem counterintuitive, as it implies a larger number resulting from a smaller base. This article will delve deep into solving this problem, explaining the underlying principles, providing multiple approaches to the solution, and exploring the broader implications of percentage calculations. We'll also look at practical examples and address common misconceptions. This comprehensive guide will equip you with the tools to tackle similar percentage problems with confidence.
Meta Description: Learn how to calculate what percent of 2 is 8. This in-depth guide explains the process, provides multiple solution methods, explores practical applications, and clarifies common misconceptions about percentages.
Understanding Percentages: The Foundation
Before jumping into the solution, let's establish a clear understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using the Percentage Formula
The most common way to solve percentage problems involves using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In our problem, "What percent of 2 is 8?", we need to identify the "part," the "whole," and then solve for the percentage.
- Part: This represents the value we're comparing to the whole. In this case, the part is 8.
- Whole: This represents the total value or the base amount. Here, the whole is 2.
Substituting these values into the formula:
(8 / 2) x 100 = Percentage
This simplifies to:
4 x 100 = 400%
Therefore, 8 is 400% of 2. This result might seem surprising at first, but it's perfectly valid. It means that 8 is four times larger than 2.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent our problem as follows:
x/100 = 8/2
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
2x = 800
Then, divide both sides by 2:
x = 400
This confirms that 8 is 400% of 2. The proportion method provides a clear visual representation of the relationship between the values.
Method 3: Working with Decimals
We can also approach this problem using decimals. First, we find the ratio of the part to the whole:
8 / 2 = 4
This means that 8 is 4 times larger than 2. To express this as a percentage, we multiply by 100:
4 x 100 = 400%
This method highlights the direct relationship between the ratio and the percentage.
Addressing the Counterintuitive Result: Percentages Greater Than 100%
The result of 400% might seem unusual because we're often accustomed to percentages between 0% and 100%. However, percentages greater than 100% are perfectly valid and represent values that exceed the whole. In our example, 8 is more than 2, indicating a percentage greater than 100%. This highlights the versatility of percentages in representing various proportions, including those exceeding the base value.
Practical Applications of Percentage Calculations Exceeding 100%
Percentages greater than 100% are commonly used in various real-world scenarios:
- Financial Growth: If a company's profit increases from $2 million to $8 million, the increase is 400% of the original profit.
- Population Increase: If a town's population grows from 2,000 to 8,000, the population increase represents a 400% growth.
- Production Increases: If a factory increases its production from 2 units to 8 units, the increase is 400% of the original production.
- Inflation Rates: A substantial inflation rate could result in prices increasing by more than 100%.
Common Mistakes and How to Avoid Them
When calculating percentages, several common mistakes can lead to incorrect results:
- Confusing the Part and the Whole: Always carefully identify which value represents the part and which represents the whole before applying the formula.
- Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations.
- Failing to Convert to Percentage: After calculating the ratio, remember to multiply by 100 to express the result as a percentage.
Expanding the Understanding: Reverse Percentage Problems
The problem "What percent of 2 is 8?" can be reversed. For example, we could ask: "2 is what percent of 8?" In this case, the part is 2, and the whole is 8. Applying the formula:
(2 / 8) x 100 = 25%
This illustrates the importance of clearly identifying the part and the whole in percentage problems.
Conclusion: Mastering Percentage Calculations
This in-depth exploration of the problem "What percent of 2 is 8?" has demonstrated that percentages are powerful tools for expressing proportions. We've examined three different methods for solving this seemingly simple yet insightful problem, highlighted the validity of percentages exceeding 100%, and discussed practical applications and common errors. By understanding the underlying principles and applying the correct formulas and methods, you can confidently tackle a wide range of percentage problems, regardless of whether the result is less than, equal to, or greater than 100%. The ability to confidently work with percentages is a crucial skill applicable across various fields, from finance and business to science and everyday life. Remember to always clearly define the 'part' and the 'whole' and choose the calculation method that best suits your understanding. Practice makes perfect, so continue applying these concepts to various percentage problems to build proficiency and confidence.
Latest Posts
Latest Posts
-
Why Are Saturated Fats Solid At Room Temperature
Apr 17, 2025
-
Cuantas Oz Hay En Un Galon
Apr 17, 2025
-
Proteins Are Made Up Of Monomers Called
Apr 17, 2025
-
Is 63 A Prime Number Or A Composite Number
Apr 17, 2025
-
How Many Centimeters Is 50 Inches
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 2 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.