What Percent Of 20 Is 12
Kalali
Apr 14, 2025 · 4 min read
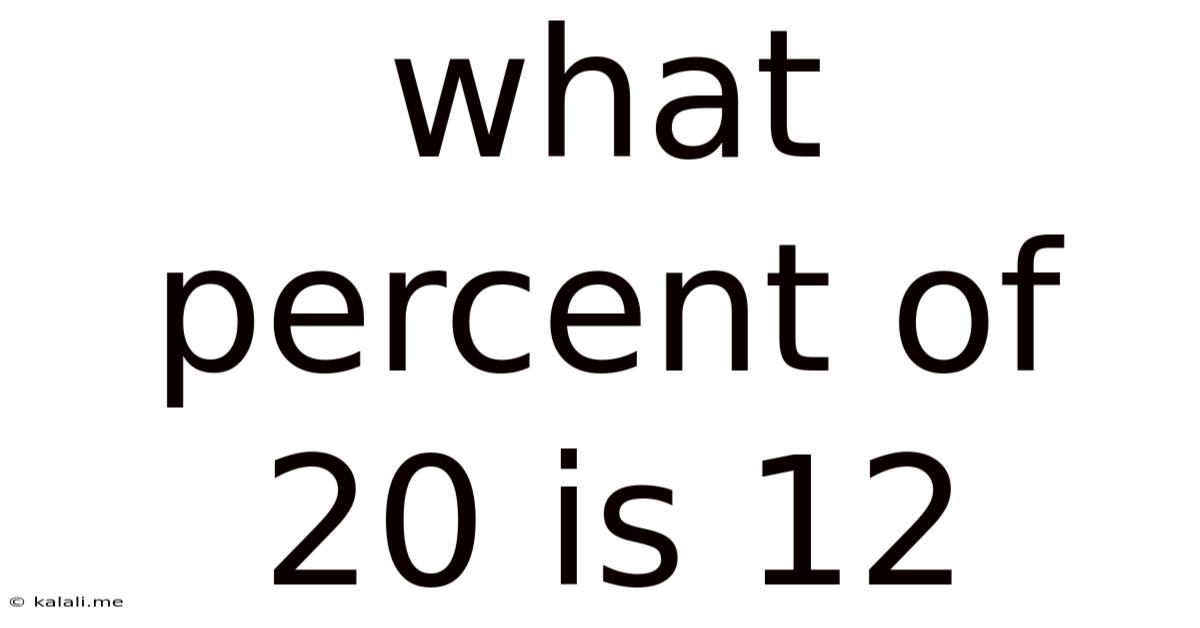
Table of Contents
What Percent of 20 is 12? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article delves into the calculation of "What percent of 20 is 12?", exploring different methods, providing step-by-step instructions, and demonstrating practical applications. We'll also look at variations of this problem and how to tackle them effectively. This detailed guide aims to solidify your understanding of percentage calculations and equip you with the tools to confidently solve similar problems.
Understanding Percentages:
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using Proportions
This method utilizes the concept of ratios and proportions to solve percentage problems. We can set up a proportion to represent the problem:
- Part/Whole = Percentage/100
In our problem, "What percent of 20 is 12?", we have:
- Part = 12
- Whole = 20
- Percentage = x (what we need to find)
Substituting these values into the proportion, we get:
12/20 = x/100
To solve for x, we cross-multiply:
12 * 100 = 20 * x
1200 = 20x
Now, divide both sides by 20:
x = 1200 / 20
x = 60
Therefore, 12 is 60% of 20.
Method 2: Using Decimal Conversion
This method involves converting the fraction representing the part to a decimal and then multiplying by 100 to express it as a percentage.
First, express the problem as a fraction:
12/20
Next, divide the numerator (12) by the denominator (20):
12 ÷ 20 = 0.6
Finally, multiply the decimal by 100 to express it as a percentage:
0.6 * 100 = 60%
Again, we arrive at the conclusion that 12 is 60% of 20.
Method 3: Using the Percentage Formula
This method directly applies the percentage formula:
Percentage = (Part / Whole) * 100
Plugging in the values from our problem:
Percentage = (12 / 20) * 100
Percentage = 0.6 * 100
Percentage = 60%
This method provides a concise and straightforward approach to solving percentage problems.
Practical Applications and Variations:
The ability to calculate percentages has numerous practical applications:
-
Discounts: A store offers a 20% discount on an item priced at $50. To calculate the discount, we find 20% of $50: (20/100) * $50 = $10. The discounted price is $50 - $10 = $40.
-
Sales Tax: A 6% sales tax is added to a $75 purchase. The tax amount is (6/100) * $75 = $4.50. The total cost is $75 + $4.50 = $79.50.
-
Tip Calculation: A 15% tip on a $100 restaurant bill is calculated as (15/100) * $100 = $15.
-
Grade Calculation: A student scores 45 out of 60 on a test. To find the percentage score, we calculate (45/60) * 100 = 75%.
-
Financial Analysis: Analyzing financial statements often involves calculating percentages to understand growth rates, profit margins, and other key metrics.
Variations of the Problem:
The problem "What percent of 20 is 12?" can be presented in several different ways, all requiring similar calculation methods:
-
"12 is what percent of 20?" This phrasing directly asks for the percentage.
-
"Find the percentage that 12 represents of 20." This is a more formal way of stating the problem.
-
"What percentage of 20 equals 12?" This phrasing focuses on the result of the percentage calculation.
Understanding these variations is important to accurately interpret and solve percentage problems presented in different contexts.
Advanced Applications and Further Learning:
Beyond the basic calculations, understanding percentages becomes crucial in more advanced mathematical concepts:
-
Compound Interest: Calculating compound interest involves understanding how percentages accumulate over time.
-
Statistical Analysis: Percentages are widely used in descriptive statistics to represent proportions and frequencies within data sets.
-
Probability and Statistics: Probability calculations often involve expressing chances as percentages.
Solving Similar Problems:
Let's practice with a few similar problems:
-
What percent of 50 is 25? Using any of the methods above, the answer is 50%.
-
What percent of 30 is 15? The answer is 50%.
-
What percent of 100 is 75? The answer is 75%.
These examples demonstrate the versatility and consistent application of percentage calculation methods.
Conclusion:
Calculating "What percent of 20 is 12?" is a straightforward process with multiple solution methods. Mastering these methods is essential for everyday tasks and advanced mathematical applications. Whether using proportions, decimal conversion, or the direct percentage formula, the answer remains consistent: 12 is 60% of 20. By understanding the underlying principles and practicing with variations, you can confidently approach and solve a wide range of percentage problems. Remember that consistent practice and applying these methods to real-world scenarios will reinforce your understanding and build your proficiency in this crucial mathematical skill. This comprehensive guide provides a solid foundation for mastering percentage calculations, enabling you to confidently tackle similar problems in various contexts.
Latest Posts
Latest Posts
-
Cuanto Es 1 50 Cm En Pies
Apr 16, 2025
-
How Many Meters Is 17 Feet
Apr 16, 2025
-
3 Is What Percent Of 14
Apr 16, 2025
-
What Is 25 Off Of 500
Apr 16, 2025
-
Is The Venus Forces More Powerful Than
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 20 Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.