What Percent Of 20 Is 5
Kalali
Apr 18, 2025 · 5 min read
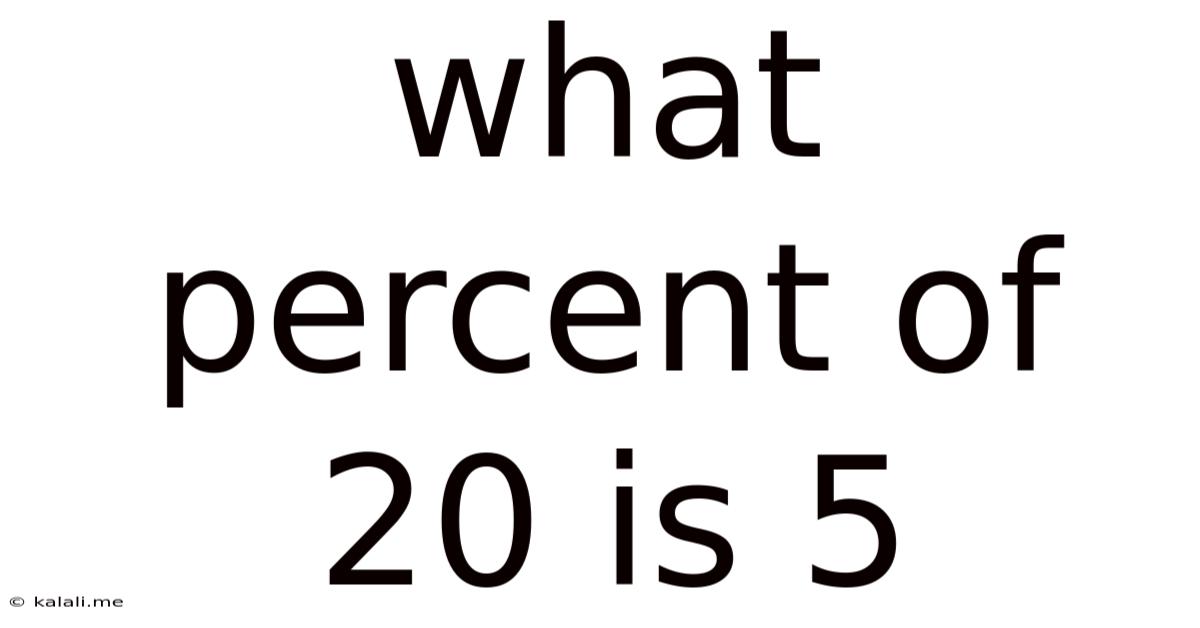
Table of Contents
What Percent of 20 is 5? A Deep Dive into Percentages and Their Applications
Finding what percent of 20 is 5 might seem like a simple arithmetic problem, but understanding the underlying concepts opens the door to a world of practical applications in various fields. This article will not only solve this specific problem but also explore the broader context of percentages, their calculation methods, and their importance in everyday life and professional settings. We'll delve into different approaches to solving percentage problems, including the use of proportions, equations, and even mental math techniques. The goal is to equip you with a comprehensive understanding of percentages, enabling you to tackle similar problems with confidence and apply this knowledge to real-world scenarios.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". Understanding this basic definition is crucial to solving any percentage problem. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or the decimal 0.5.
Solving "What Percent of 20 is 5?"
There are several methods to determine what percentage 5 represents of 20. Let's explore the most common approaches:
Method 1: Using Proportions
This method involves setting up a proportion, which is an equation that states that two ratios are equal. We can set up the proportion as follows:
- x/100 = 5/20
Here:
- 'x' represents the percentage we want to find.
- 5 is the part.
- 20 is the whole.
To solve for 'x', we cross-multiply:
- 20x = 500
Then, divide both sides by 20:
- x = 25
Therefore, 5 is 25% of 20.
Method 2: Using an Equation
We can also solve this using a simple equation. The basic formula for percentage problems is:
- (Part / Whole) * 100 = Percentage
Substituting the values from our problem:
- (5 / 20) * 100 = Percentage
This simplifies to:
- (0.25) * 100 = 25
Again, we find that 5 is 25% of 20.
Method 3: Mental Math (for simpler problems)
For simpler problems like this, mental math can be a quick and efficient approach. Since 5 is half of 10, and 10 is half of 20, we can reason that 5 is one-quarter (or 25%) of 20. This method relies on recognizing relationships between numbers and is particularly useful for quick estimations.
Expanding the Understanding: Real-World Applications of Percentages
The ability to calculate percentages is a fundamental skill with wide-ranging applications in various aspects of daily life and professional settings. Let’s explore some examples:
1. Finance and Budgeting:
- Calculating interest rates: Understanding percentages is crucial for understanding interest rates on loans, savings accounts, credit cards, and investments. Knowing how to calculate interest earned or paid helps make informed financial decisions.
- Analyzing financial statements: Percentages are used extensively in analyzing financial statements like income statements and balance sheets. Ratios like profit margins, debt-to-equity ratios, and return on investment (ROI) are all expressed as percentages, providing valuable insights into a company’s financial health.
- Calculating discounts and sales tax: When shopping, percentages are used to calculate discounts and sales tax. Understanding these calculations helps budget effectively and ensure you're getting the best deals.
- Tracking personal finances: Budgeting involves allocating a percentage of your income to different categories, like housing, food, transportation, and entertainment. This aids in financial planning and helps you stay within your budget.
2. Science and Statistics:
- Expressing probabilities: Probabilities are often expressed as percentages, representing the likelihood of an event occurring. For instance, a weather forecast might state a 70% chance of rain.
- Analyzing data: Percentages are used in various statistical analyses to summarize and present data in a more meaningful way. They help compare different groups and identify trends.
- Scientific experiments: Percentages are commonly used in expressing the results of scientific experiments, such as the percentage of successful trials or the percentage change in a measured variable.
3. Business and Marketing:
- Pricing strategies: Businesses use percentages to determine pricing strategies, calculate markups, and offer discounts. Understanding cost-plus pricing and margin calculations is essential for setting profitable prices.
- Market share analysis: Market share is often expressed as a percentage, indicating the proportion of a market that a company or product controls. This analysis helps assess a company’s competitive position.
- Sales and conversion rates: Businesses use percentages to track sales and conversion rates, which measure the effectiveness of marketing campaigns and sales efforts.
4. Education and Academia:
- Calculating grades: Grades are often expressed as percentages, representing the proportion of correct answers or the overall performance in a course.
- Assessing student progress: Teachers and educators use percentages to monitor student progress and identify areas where students may need additional support.
5. Everyday Life:
- Cooking and baking: Recipes often involve percentages when scaling up or down.
- Tipping in restaurants: Calculating tips often involves determining a percentage of the total bill.
- Understanding nutritional information: Nutritional labels use percentages to represent the daily recommended intake of various nutrients.
Advanced Percentage Calculations and Problem-Solving Techniques
Beyond the basic percentage calculations, several more advanced techniques can help solve complex problems:
- Finding the whole when the percentage and part are known: If you know that 25% of a number is 5, you can use the equation: (Part / Percentage) * 100 = Whole. This helps determine the original value.
- Finding the part when the percentage and whole are known: If you know that 20% of 100 is 'x', you can calculate 'x' by: (Percentage / 100) * Whole = Part.
- Percentage increase and decrease: These calculations involve finding the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is similar, with a negative value indicating a decrease.
- Compound percentages: These are percentages applied multiple times, such as compound interest. They require more complex calculations and understanding of exponential growth.
Conclusion:
Determining what percent of 20 is 5, while seemingly straightforward, serves as a springboard for understanding the wider applications of percentages. Mastering percentage calculations is a valuable skill applicable to various fields, from finance and business to science and everyday life. The methods discussed—proportions, equations, and mental math—offer versatile approaches to solving percentage problems, allowing for flexibility and efficiency depending on the complexity of the problem. By understanding the underlying principles and practicing different calculation techniques, you can develop confidence and proficiency in working with percentages, enabling you to tackle more complex challenges and make informed decisions in various contexts.
Latest Posts
Latest Posts
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
-
500 Ml Is How Many Cups Of Water
Apr 19, 2025
-
15 Of What Number Is 6
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 20 Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.