What Percent Of 25 Is 16
Kalali
Apr 28, 2025 · 4 min read
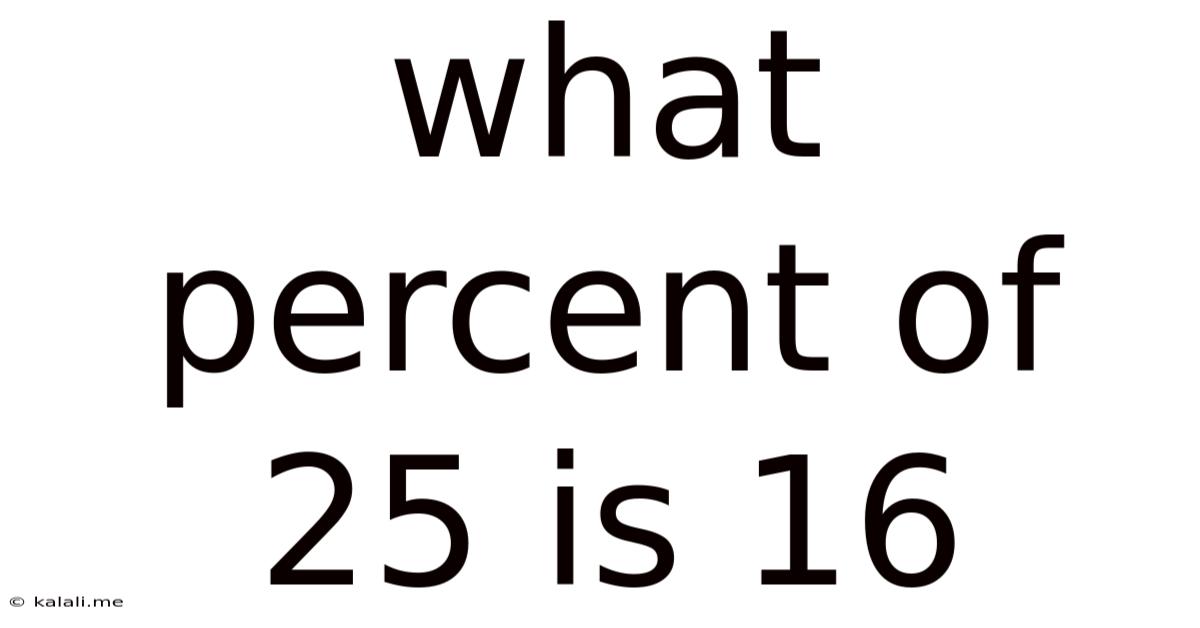
Table of Contents
What Percent of 25 is 16? A Comprehensive Guide to Percentage Calculations
This article delves into the seemingly simple question: "What percent of 25 is 16?" While the answer might seem straightforward, understanding the underlying principles of percentage calculations is crucial for various applications in math, finance, and everyday life. This guide will not only provide the solution but also explain the methodology, offer alternative approaches, and explore related percentage problems. We'll even touch upon practical real-world examples to solidify your understanding.
Understanding Percentages: The Foundation
Before diving into the specific problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. They're vital in finance (interest rates, discounts), statistics (data representation), and everyday scenarios (tips, sales tax).
Method 1: Setting up a Proportion
The most common approach to solving "What percent of 25 is 16?" is by setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion as follows:
- x/100 = 16/25
Where:
- x represents the unknown percentage we're trying to find.
- 16/25 represents the fraction of 16 out of 25.
To solve for x, we can cross-multiply:
- 25x = 1600
Then, divide both sides by 25:
- x = 1600 / 25 = 64
Therefore, 16 is 64% of 25.
Method 2: Using the Formula
Alternatively, we can use a direct formula to calculate percentages. The general formula for finding what percentage one number (Part) is of another number (Whole) is:
- Percentage = (Part / Whole) * 100
In our problem:
- Part = 16
- Whole = 25
Substituting these values into the formula:
- Percentage = (16 / 25) * 100 = 0.64 * 100 = 64%
This method provides the same result as the proportion method, confirming our answer.
Method 3: Decimal Conversion and Multiplication
This method involves converting the fraction 16/25 into a decimal and then multiplying by 100 to express it as a percentage.
First, divide 16 by 25:
- 16 / 25 = 0.64
Next, multiply the decimal by 100:
- 0.64 * 100 = 64%
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in numerous real-world scenarios. Let's explore some examples:
-
Sales and Discounts: A store offers a discount of $9 on an item originally priced at $25. What is the percentage discount? Using the formula: (9/25) * 100 = 36%. The store is offering a 36% discount.
-
Calculating Tips: You had dinner at a restaurant and the bill was $25. You want to leave a 20% tip. How much should you tip? 20% of $25 is (20/100) * 25 = $5.
-
Grade Calculation: You scored 16 out of 25 points on a quiz. What is your percentage score? Using the familiar method: (16/25) * 100 = 64%. You achieved a score of 64%.
-
Financial Analysis: A company's profit increased from $16 million to $25 million. What is the percentage increase? This requires a slightly different calculation: [(25-16)/16] * 100 = 56.25%. The profit increased by 56.25%.
Solving Related Percentage Problems
Now that we've mastered finding what percent one number is of another, let's expand our skills by exploring some related problems:
-
Finding a Percentage of a Number: What is 64% of 25? This is the reverse of our original problem. The solution is (64/100) * 25 = 16.
-
Finding the Whole when a Percentage is Known: 64% of a number is 16. What is the number? This involves setting up an equation: 0.64 * x = 16. Solving for x, we get x = 16 / 0.64 = 25.
-
Percentage Change (Increase or Decrease): Calculating the percentage change involves finding the difference between two values, dividing it by the original value, and then multiplying by 100. For example, if a value increases from 20 to 25, the percentage increase is [(25-20)/20] * 100 = 25%.
Advanced Percentage Concepts:
For those wanting to delve deeper into percentage calculations, consider exploring these advanced concepts:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
-
Percentage Points vs. Percentages: It's important to distinguish between percentage points and percentages. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original value.
-
Working with Multiple Percentages: Calculating consecutive percentages, such as applying discounts one after another, requires careful consideration of the order and application of the percentages.
Conclusion
The question "What percent of 25 is 16?" serves as a gateway to understanding the fundamental principles of percentage calculations. Mastering this seemingly simple problem equips you with the skills to tackle a wide range of percentage-related problems in diverse fields. By understanding the various methods and practical applications discussed in this article, you can confidently approach and solve percentage problems in your academic pursuits, professional life, and everyday encounters. Remember, consistent practice is key to mastering these essential mathematical concepts. So, grab a calculator, work through some examples, and solidify your understanding of percentages!
Latest Posts
Latest Posts
-
160 Cm Is How Many Feet
Apr 28, 2025
-
4 2 5 As An Improper Fraction
Apr 28, 2025
-
How Many Meters Is 400 Ft
Apr 28, 2025
-
How Many Ft Is 50 Cm
Apr 28, 2025
-
What Is 5 And 3 8 As A Decimal
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 25 Is 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.