What Percent Of 28 Is 35
Kalali
Apr 25, 2025 · 5 min read
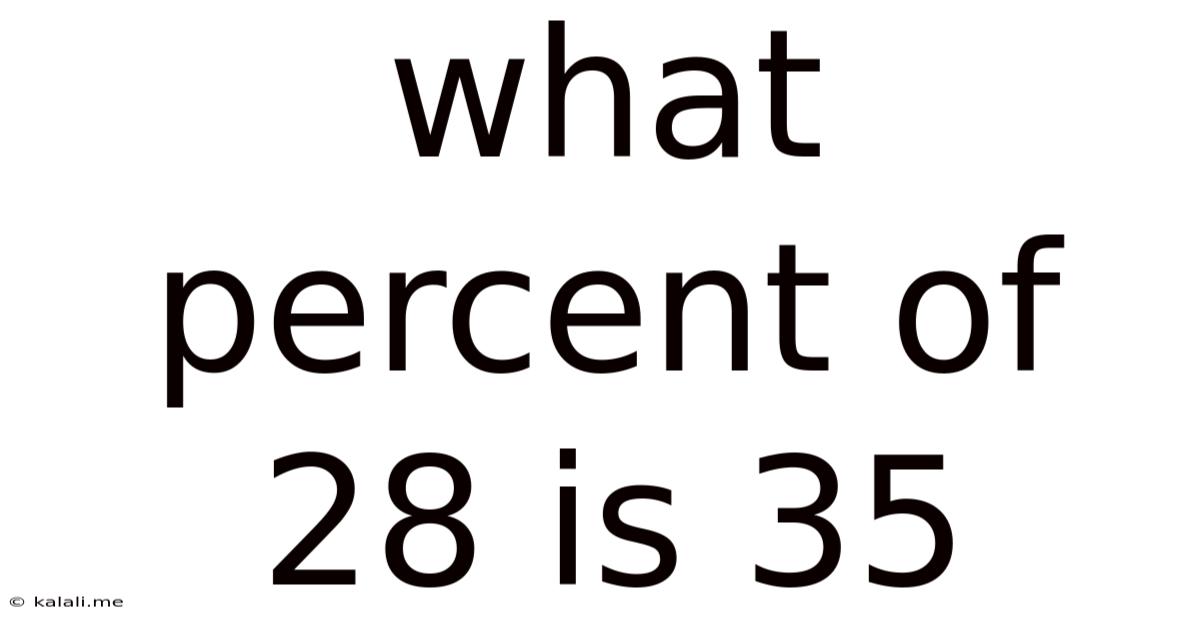
Table of Contents
What Percent of 28 is 35? Unlocking the Power of Percentage Calculations
This seemingly simple question – "What percent of 28 is 35?" – opens the door to a world of practical applications in various fields, from calculating discounts and taxes to understanding statistics and financial reports. This article will not only answer the question directly but also delve into the underlying principles of percentage calculations, providing you with the tools to tackle similar problems confidently. We'll explore different methods, discuss the importance of understanding percentages, and illustrate their relevance in everyday life.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is key to mastering percentage calculations. Percentages are used extensively to represent proportions, changes, and rates in various contexts.
Method 1: Setting up a Proportion
The most straightforward method for solving "What percent of 28 is 35?" involves setting up a proportion. A proportion is an equation that states that two ratios are equal. In this case, we can set up the following proportion:
x/100 = 35/28
Where 'x' represents the percentage we are trying to find. We can solve for 'x' by cross-multiplying:
28x = 3500
Now, divide both sides by 28:
x = 3500 / 28 = 125
Therefore, 35 is 125% of 28. This indicates that 35 is larger than 28; hence, the percentage is greater than 100%.
Method 2: Using the Percentage Formula
The percentage formula provides another effective approach. The basic formula is:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 35 (the value we're comparing)
- Whole: 28 (the base value)
Substituting these values into the formula:
Percentage = (35 / 28) * 100 = 1.25 * 100 = 125%
Again, we arrive at the answer: 35 is 125% of 28.
Method 3: Understanding the Concept of Increase
This method helps visualize the problem. Since 35 is larger than 28, we're dealing with a percentage increase. We can calculate the increase as follows:
Increase = 35 - 28 = 7
Now, we find what percentage of 28 this increase represents:
Percentage Increase = (Increase / Original Value) * 100 = (7 / 28) * 100 = 0.25 * 100 = 25%
This means 35 is 25% more than 28. Adding this increase to the original 100% (of 28) gives us 125%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a crucial skill applicable in numerous everyday situations:
-
Financial Calculations: Calculating interest rates, discounts, taxes, tips, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes in stock prices or investment portfolios is essential for informed financial decisions. Calculating compound interest, a cornerstone of financial growth, uses percentage calculations repeatedly.
-
Statistics and Data Analysis: Percentages are fundamental to interpreting statistical data. They help represent proportions within datasets, enabling comparisons and identifying trends. For instance, understanding market share percentages, survey results, or demographic breakdowns relies on the accurate calculation and interpretation of percentages. Understanding percentage points vs. percentage change is critical in this context.
-
Retail and Sales: Calculating discounts, sales tax, and markups are core components of retail operations. Understanding percentage-based pricing strategies is crucial for both businesses and consumers.
-
Science and Engineering: Many scientific and engineering calculations involve percentages. For example, calculating efficiency, error rates, or concentrations often requires working with percentages.
-
Everyday Life: From calculating cooking proportions to understanding nutritional information on food labels, percentages are integrated into numerous aspects of our daily routines.
Beyond the Basics: Advanced Percentage Calculations
While the problem "What percent of 28 is 35?" is relatively straightforward, percentage calculations can become more complex. Here are some advanced concepts:
-
Percentage Change: This calculates the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. This is crucial for tracking growth or decline in various metrics.
-
Compound Percentage: This calculates the effect of applying a percentage change multiple times. It's particularly relevant in financial calculations, such as compound interest, where interest earned is added to the principal, and subsequent interest is calculated on the larger amount.
-
Percentage Points: A percentage point refers to an absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Inverse Percentage Problems: These involve finding the original value when given a percentage and the resulting value. For example, "A product is on sale for 20% off and costs $60. What was the original price?" requires working backwards using the percentage formula.
Mastering Percentages: Tips and Practice
To solidify your understanding of percentage calculations, consider these tips:
-
Practice Regularly: The more you practice, the more comfortable and efficient you'll become.
-
Use Different Methods: Experiment with the proportion method, the percentage formula, and the increase/decrease approach to find the method that suits you best.
-
Visualize the Problem: Draw diagrams or use real-world examples to aid your understanding.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
By understanding the fundamental principles of percentage calculations and practicing regularly, you'll equip yourself with a powerful tool for solving various problems across diverse fields. Remember, mastering percentages isn't just about solving mathematical problems; it's about developing a critical thinking skill applicable in numerous aspects of life. So, the next time you encounter a percentage problem – whether it's calculating a discount or analyzing statistical data – you'll be ready to tackle it with confidence.
Latest Posts
Latest Posts
-
2 3 Cup Of Milk In Ml
Apr 25, 2025
-
How Long Is 41 Inches In Feet
Apr 25, 2025
-
What Is The Square Root Of 2025
Apr 25, 2025
-
1 Percent Of 1 Million Dollars
Apr 25, 2025
-
Inverse Of 1 To 1 Function
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 28 Is 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.