What Percent Of 28 Is 7
Kalali
Apr 14, 2025 · 5 min read
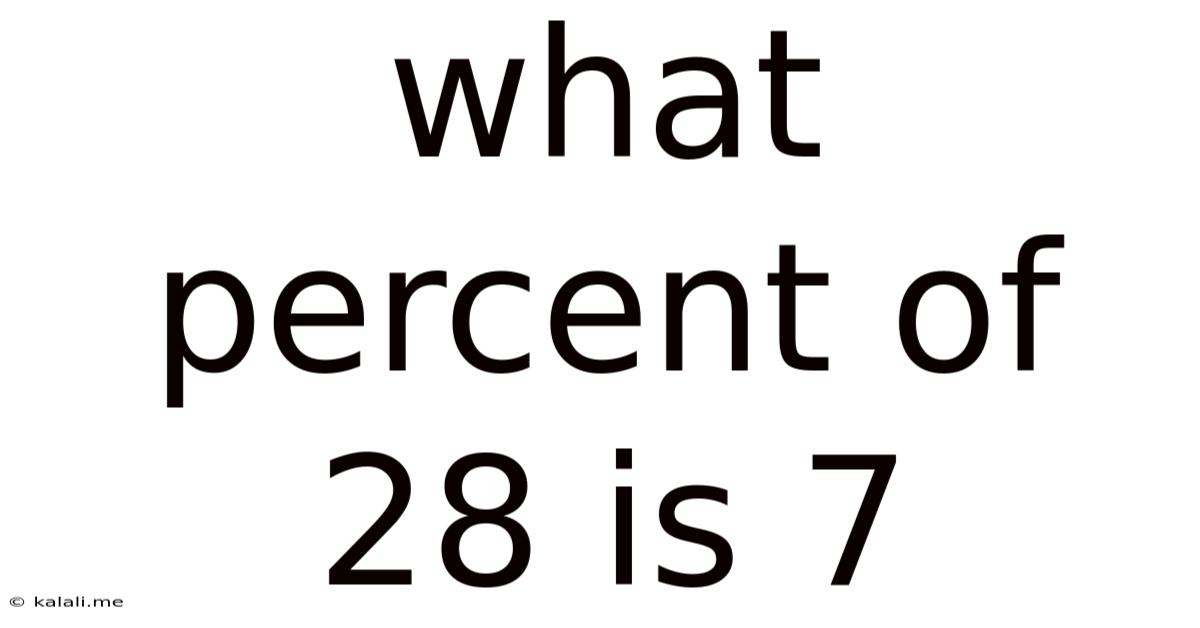
Table of Contents
What Percent of 28 is 7? A Deep Dive into Percentage Calculations
Meta Description: Learn how to calculate percentages, understand the concept of "what percent of 28 is 7," and explore different methods for solving similar problems. This comprehensive guide covers basic percentage calculations, real-world applications, and advanced techniques.
This seemingly simple question, "What percent of 28 is 7?", opens the door to a much broader understanding of percentage calculations – a fundamental skill in mathematics with countless real-world applications. While the answer might seem immediately obvious to some, mastering the underlying principles allows us to tackle more complex percentage problems with ease and confidence. This article will not only provide the solution but also delve into the various methods for calculating percentages, exploring different approaches and showcasing their versatility.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent percentages. Understanding this foundational concept is crucial for solving any percentage problem. For example, 50% means 50 out of 100, which simplifies to ½ or 0.5 as a decimal.
Method 1: The Proportion Method
This method utilizes the concept of proportions – two equivalent ratios. We can set up a proportion to solve "What percent of 28 is 7?" as follows:
-
Let x represent the unknown percentage.
-
The proportion can be written as: x/100 = 7/28
-
Cross-multiply: 28x = 700
-
Solve for x: x = 700/28 = 25
-
Therefore, 7 is 25% of 28.
This method is straightforward and easily adaptable to various percentage problems. It clearly illustrates the relationship between the parts and the whole.
Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then using multiplication. We start by converting the percentage (which we'll find) to its decimal equivalent. Let's represent this as "x". The equation becomes:
-
x * 28 = 7
-
To solve for x, divide both sides by 28: x = 7/28 = 0.25
-
To convert the decimal back to a percentage, multiply by 100: 0.25 * 100 = 25%
-
Therefore, 7 is 25% of 28.
This method is concise and efficient, especially when working with calculators.
Method 3: The Formula Method
A more generalized formula approach can be used for solving any "what percent of x is y" problem. The formula is:
- (y/x) * 100 = Percentage
In our case:
- (7/28) * 100 = 25%
This formula provides a direct and systematic approach to calculating percentages. It's particularly helpful when dealing with more complex problems or when working without a calculator.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a vital skill in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. Understanding how to calculate compound interest, for example, is crucial for effective financial planning. Determining the percentage increase or decrease in a stock price is also critical for investors.
-
Retail and Sales: Discounts, sales tax, markups, and profit percentages are integral parts of retail operations. Salespeople need to quickly calculate discounts and final prices, and managers need to analyze sales data expressed as percentages. Understanding these concepts is important for both customers and businesses.
-
Science and Statistics: Percentages are extensively used in scientific research and statistical analysis to represent data and draw conclusions. Expressing experimental results as percentages, calculating error margins, and understanding statistical significance are all crucial steps in scientific endeavors. Many scientific studies present findings as percentages.
-
Data Analysis: In data analysis, understanding percentages is essential for interpreting data trends and patterns. Representing data as percentages allows for easy comparisons across different categories. Analysts regularly use percentages to visualize data trends and provide informed insights.
-
Everyday Life: From calculating tips in restaurants to understanding the nutritional value of food (e.g., percentage of daily recommended value), percentages are ubiquitous in everyday life. Understanding percentages helps make informed decisions in various everyday situations.
Advanced Percentage Problems
While "What percent of 28 is 7?" is a relatively simple problem, the techniques discussed can be applied to more complex scenarios:
-
Finding the original amount: If you know that 25% of a number is 7, you can use the same techniques to find the original number (28). The reverse calculation involves solving an equation.
-
Calculating percentage increase or decrease: Finding the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100. This is often used to track changes in sales figures, populations, or stock prices.
-
Compound interest calculations: Compound interest calculations involve repeated percentage calculations over multiple periods. The formula involves a more complex calculation, but it still relies on the foundational understanding of percentages.
Practical Tips for Mastering Percentage Calculations
-
Practice regularly: Consistent practice is key to mastering percentage calculations. Start with simple problems and gradually move towards more complex ones.
-
Use visual aids: Diagrams and charts can help visualize percentages and improve understanding.
-
Utilize online resources: Many online calculators and tutorials can assist in solving percentage problems.
-
Understand the context: Always pay attention to the context of the problem to ensure you're applying the correct method.
Conclusion
The question "What percent of 28 is 7?" provides a starting point for a comprehensive exploration of percentage calculations. Understanding the different methods – proportion, decimal, and formula methods – allows for flexible problem-solving. This fundamental mathematical skill has broad applications across various disciplines and everyday life, making it crucial for effective problem-solving and informed decision-making. By mastering these techniques and practicing regularly, you can confidently tackle any percentage problem, from the simplest to the most complex. Remember to always check your work and ensure your answer is logical within the context of the problem. The more you practice, the more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
Select All Correct Features Of Reptile Reproduction
Apr 15, 2025
-
What Is 18 As A Fraction
Apr 15, 2025
-
Cuanto Es 8 Metros En Pies
Apr 15, 2025
-
Which Is A Gas At Room Temperature Sodium
Apr 15, 2025
-
How Many Cups Are In 30 Oz
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 28 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.