What Percent Of 30 Is 400
Kalali
Apr 16, 2025 · 5 min read
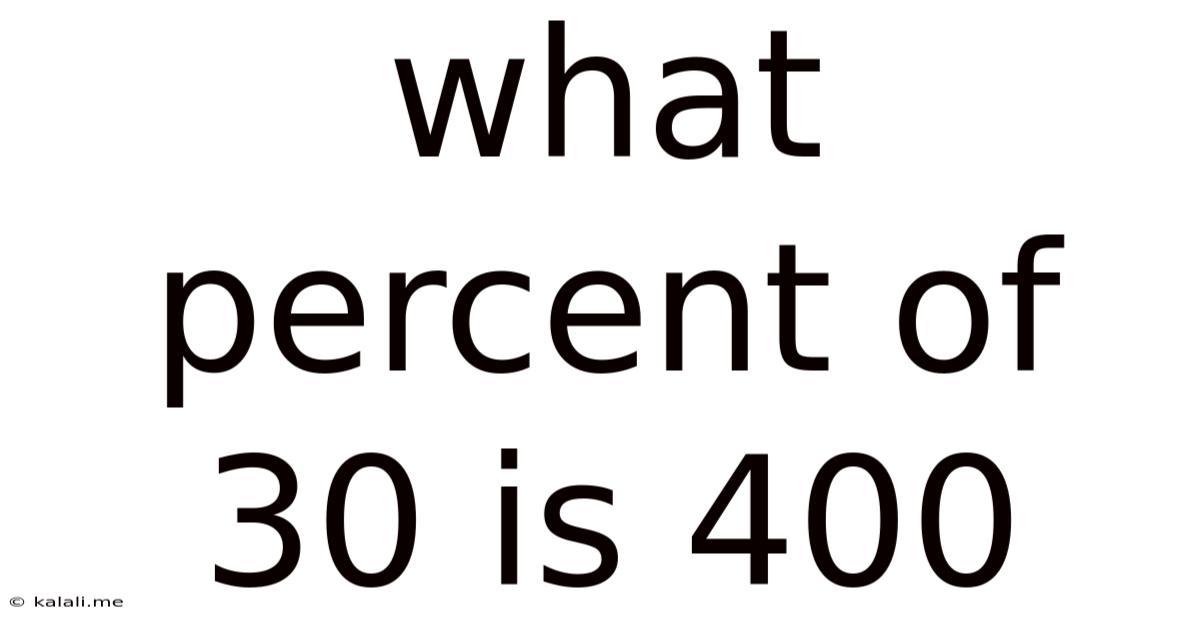
Table of Contents
What Percent of 30 is 400? Understanding Percentage Calculations and Their Applications
This seemingly simple question, "What percent of 30 is 400?", actually opens the door to a broader understanding of percentage calculations, their real-world applications, and how to solve similar problems efficiently. At first glance, it might seem counterintuitive that a smaller number (30) could somehow represent a percentage of a larger number (400). However, understanding the underlying principles will clarify this and equip you with the tools to tackle similar percentage problems with confidence. This article will not only answer the initial question but will also delve into the methodology, provide practical examples, and explore various methods for solving percentage problems.
Meta Description: Discover how to calculate percentages, understand the concept of "what percent of 30 is 400?", and explore diverse applications of percentage calculations in everyday life and various fields. Learn different methods and formulas to solve percentage problems effectively.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ("per cent" is derived from the Latin "per centum"). This concept is fundamental to understanding how to solve percentage problems. We use percentages to represent parts of a whole, allowing for easy comparison and comprehension of proportions. For instance, 50% represents 50 parts out of 100, which simplifies to 1/2 or 0.5.
Solving "What Percent of 30 is 400?"
The question, "What percent of 30 is 400?", requires us to find the percentage that 400 represents when compared to 30. This is not a typical percentage problem where a percentage of a number is given, and we need to find the resulting value. Instead, we're working backward.
Here's how we can solve this:
-
Set up a proportion: We can represent the problem as a proportion:
x/100 = 400/30Where 'x' represents the percentage we are trying to find.
-
Cross-multiply: To solve for 'x', we cross-multiply:
30x = 400 * 10030x = 40000 -
Solve for x: Divide both sides by 30:
x = 40000/30x = 1333.33(approximately)
Therefore, 400 is approximately 1333.33% of 30.
This result might seem surprisingly large, but it's perfectly valid. It simply means that 400 is over thirteen times larger than 30.
Alternative Methods for Solving Percentage Problems
While the proportion method is effective, several other approaches can solve percentage problems, each with its own advantages:
-
Using the formula: The basic percentage formula is:
(Part / Whole) * 100 = PercentageIn our case, 400 is the part, and 30 is the whole. Applying the formula:
(400 / 30) * 100 = 1333.33% -
Decimal conversion: You can convert the percentage to a decimal and then multiply. For instance, if we want to find 25% of 80, we convert 25% to 0.25 and multiply it by 80 (0.25 * 80 = 20). This method is particularly useful for quick mental calculations.
-
Using a calculator: Most calculators have a percentage function that simplifies the calculation significantly. Simply enter the values and use the percentage button to get the result directly.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and various fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage calculations. Understanding percentages is crucial for making informed financial decisions. For example, calculating the simple interest on a loan or the compound interest on a savings account requires precise percentage calculations.
-
Sales and Marketing: Businesses use percentages to track sales growth, customer conversion rates, market share, and discount promotions. Analyzing these metrics helps businesses understand their performance and make data-driven decisions. For instance, a 10% increase in sales over the previous year is a key performance indicator for many businesses.
-
Statistics and Data Analysis: Percentages are fundamental in representing and interpreting statistical data. They are commonly used to express proportions, probabilities, and frequencies. For example, polling data often presents results in percentages to represent the proportion of the population that holds a particular opinion.
-
Science and Engineering: Percentages are used in various scientific and engineering applications, such as calculating error margins, efficiency rates, and concentrations of solutions. For example, the percentage of a particular element in an alloy is critical information for material scientists.
-
Education: Grading systems, test scores, and performance evaluations often use percentages to assess academic achievement.
-
Everyday Life: We encounter percentages daily, such as when calculating tips in restaurants, figuring out sale discounts, understanding nutritional information on food labels, or comprehending weather forecasts (chance of rain).
Beyond the Basics: More Complex Percentage Problems
While "What percent of 30 is 400?" showcases a fundamental percentage calculation, the concept extends to more complex scenarios. For instance, you might encounter problems involving:
-
Percentage increase or decrease: Calculating the percentage change between two values. This involves finding the difference between the two values, dividing by the original value, and multiplying by 100.
-
Compound interest: Interest earned not only on the principal amount but also on accumulated interest. Compound interest calculations are more complex than simple interest calculations and require iterative calculations.
-
Percentage points: A percentage point is a unit of measurement, not a percentage itself. For instance, if interest rates increase from 5% to 7%, it’s a 2 percentage point increase, not a 40% increase (2/5 * 100 = 40%).
-
Percentage of a percentage: Calculating a percentage of a percentage requires nested calculations. For instance, finding 10% of 20% of 100 would be 10% of (20% of 100) = 10% of 20 = 2.
Mastering Percentage Calculations: Practice and Resources
The key to mastering percentage calculations is consistent practice. Start with simpler problems and gradually work your way up to more complex ones. There are numerous online resources available, including interactive calculators, practice problems, and tutorials, that can assist in developing your skills. Understanding the underlying principles and practicing regularly will make you proficient in solving diverse percentage problems.
Conclusion: The Power of Percentages
The seemingly straightforward question, "What percent of 30 is 400?", underscores the importance and versatility of percentage calculations. From managing finances to interpreting scientific data, understanding percentages is a crucial skill applicable across various fields. By mastering the methods and formulas discussed in this article, you'll not only be able to answer specific percentage questions but also gain a deeper understanding of proportions and ratios, crucial elements in various quantitative analyses. Remember, consistent practice is key to mastering percentage calculations and unlocking their full potential in your daily life and professional endeavors.
Latest Posts
Latest Posts
-
Is Carbon A Metal Or Nonmetal Or Metalloid
Apr 16, 2025
-
Non Living Things In An Ecosystem
Apr 16, 2025
-
How Many Liters In 55 Gallons
Apr 16, 2025
-
What Happens When Oceanic And Continental Crust Collide
Apr 16, 2025
-
10 Milliliters Equals How Many Ounces
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 30 Is 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.