What Percent Of 35 Is 5
Kalali
Apr 07, 2025 · 5 min read
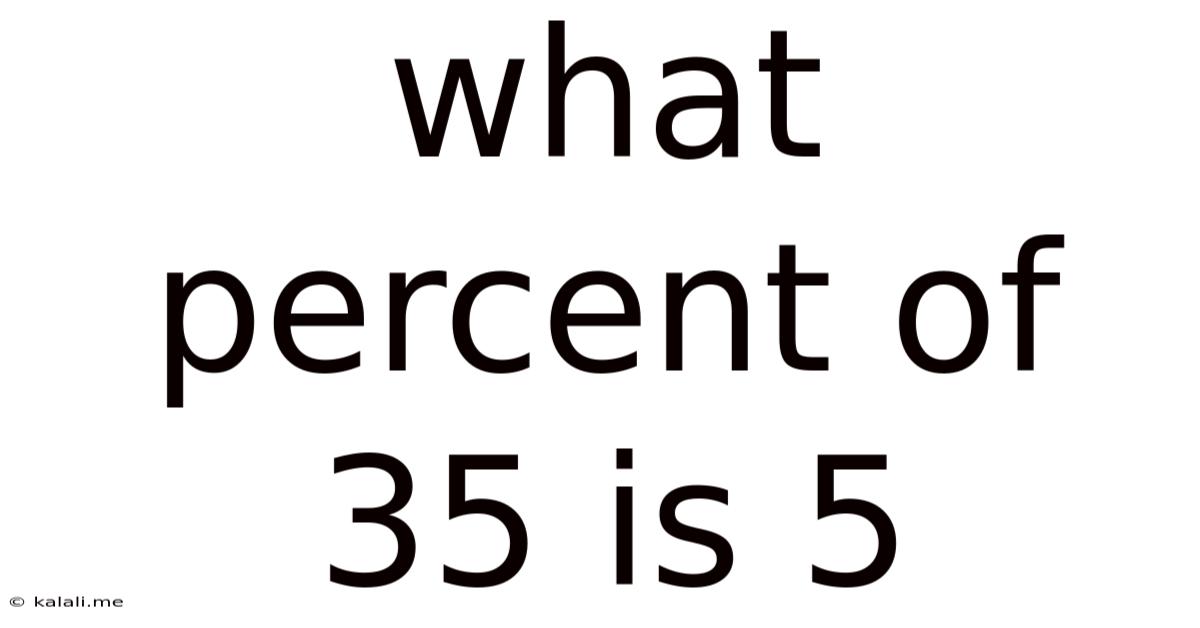
Table of Contents
What Percent of 35 is 5? A Deep Dive into Percentage Calculations
Finding what percent of 35 is 5 might seem like a simple arithmetic problem, but it's a fundamental concept with wide-ranging applications in various fields, from everyday budgeting to complex financial analysis. This article will not only provide you with the solution but will also delve into the underlying principles, explore different methods of solving percentage problems, and illustrate its relevance across diverse scenarios.
Understanding Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred," indicating the proportion of a quantity relative to the whole. For instance, 50% means 50 parts out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Calculating "What Percent of 35 is 5?"
There are several ways to solve this problem, each offering a different perspective on percentage calculations. Let's explore the most common methods:
Method 1: Using Proportions
This method leverages the fundamental principle of proportionality. We can set up a proportion where we equate two ratios:
- Ratio 1: Represents the given information: 5 is to 35 (5/35)
- Ratio 2: Represents the unknown percentage: x is to 100 (x/100)
Therefore, our proportion is: 5/35 = x/100
To solve for 'x', we cross-multiply:
5 * 100 = 35 * x
500 = 35x
x = 500/35
x ≈ 14.29
Therefore, 5 is approximately 14.29% of 35.
Method 2: Using Decimal Conversion
This method involves converting the fraction 5/35 into a decimal and then multiplying by 100 to express it as a percentage.
- Divide: 5 divided by 35 = 0.142857 (approximately)
- Multiply: 0.142857 * 100 = 14.29% (approximately)
This method confirms our previous result: 5 is approximately 14.29% of 35.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our problem:
- Part = 5
- Whole = 35
Substituting these values into the formula:
(5 / 35) * 100% = 14.29% (approximately)
This method again confirms that 5 is approximately 14.29% of 35.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
1. Finance and Budgeting:
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments requires calculating percentages. For example, if you have a savings account with a 3% annual interest rate and a balance of $1000, you can calculate your yearly interest earnings using percentage calculations.
- Discounts and Sales Tax: Calculating discounts during sales or adding sales tax to a purchase price involves percentage calculations. If a shirt is 20% off its original price of $50, knowing how to calculate the discount amount is essential.
- Investment Returns: Tracking the performance of your investments and understanding the rate of return involves calculating percentage changes in the value of your investments over time.
2. Statistics and Data Analysis:
- Data Representation: Percentages are widely used to represent data in charts, graphs, and reports. For example, presenting survey results or election outcomes often involves percentages to convey proportions effectively.
- Probability and Risk Assessment: In probability and risk assessment, percentages are used to express the likelihood of events occurring. For example, insurance companies use percentages to calculate risk probabilities and determine premiums.
3. Everyday Life:
- Tipping: Calculating the appropriate tip amount in restaurants or for services involves calculating a percentage of the total bill.
- Cooking and Baking: Adjusting recipes often requires understanding and applying percentage calculations to increase or decrease ingredient quantities.
- Comparing Prices: When comparing prices of similar products, percentage calculations can help determine the best value for your money.
Expanding on the Concept: Variations and Related Problems
While we've focused on finding what percent of 35 is 5, similar percentage problems involve finding different parts of the equation. Let's consider some variations:
- Finding the Part: "What is 14.29% of 35?" This would be solved by multiplying 0.1429 by 35.
- Finding the Whole: "5 is 14.29% of what number?" This problem requires setting up a different proportion: 5/x = 14.29/100, solving for x.
Understanding these variations is crucial for applying percentage calculations in diverse situations.
Advanced Percentage Calculations: Compound Interest and More
Beyond basic percentage calculations, more complex scenarios exist in finance involving compound interest, growth rates, and depreciation. These require a deeper understanding of exponential functions and their application to percentage change over time. For instance, calculating the future value of an investment with compound interest involves repeatedly applying percentage growth over multiple periods.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice percentage calculations, the more confident and proficient you'll become.
- Utilize Different Methods: Experiment with different methods (proportions, decimal conversion, formulas) to find the approach that resonates best with you.
- Check Your Answers: Always verify your answers using a different method to ensure accuracy.
- Understand the Context: Pay close attention to the wording of the problem to correctly identify the "part," "whole," and the unknown element.
Conclusion
Determining what percent of 35 is 5—approximately 14.29%—is more than a simple arithmetic exercise. It's a fundamental concept with widespread applications across various domains. By understanding the different methods of solving percentage problems and grasping their real-world relevance, you equip yourself with a powerful tool for navigating financial decisions, analyzing data, and tackling everyday challenges. Continuously practicing and refining your skills in percentage calculations will undoubtedly enhance your problem-solving abilities and contribute to a more informed approach to quantitative tasks.
Latest Posts
Latest Posts
-
1 Cup Of Butter To Oz
Apr 09, 2025
-
How Many Oz Is 1 3
Apr 09, 2025
-
What Is 180 Degrees Fahrenheit In Celsius
Apr 09, 2025
-
Which Expression Is Equivalent To St 6
Apr 09, 2025
-
1 000 000 In Roman Numerals
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 35 Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.