What Percent Of 4 Is 1
Kalali
Apr 11, 2025 · 5 min read
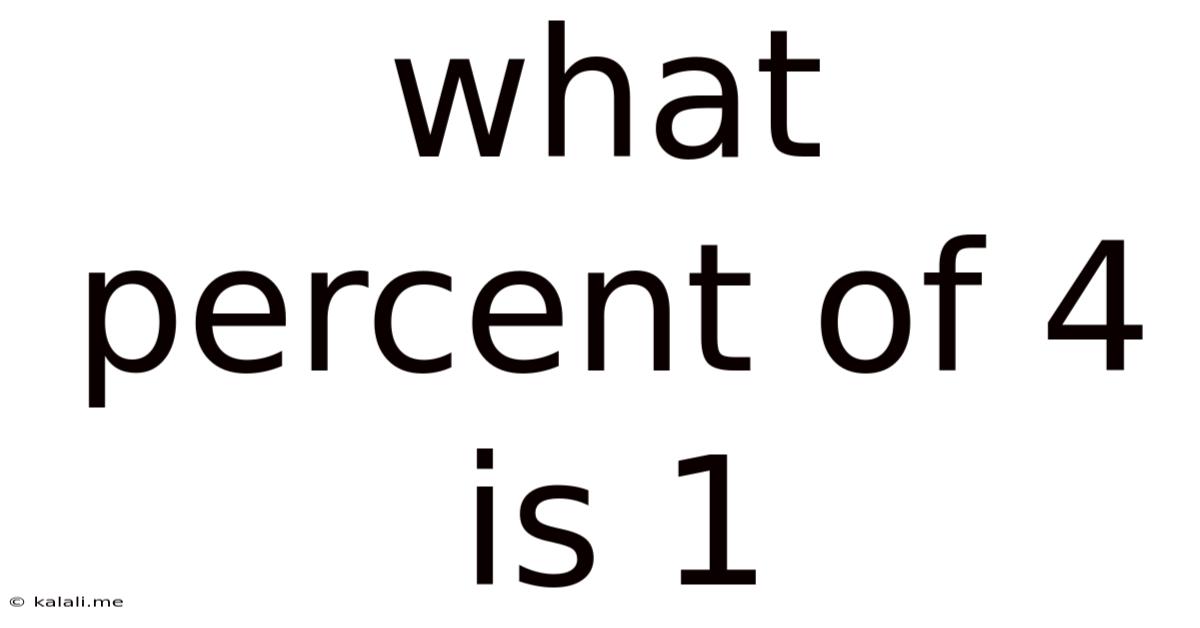
Table of Contents
What Percent of 4 is 1? Understanding Percentages and Their Applications
This seemingly simple question, "What percent of 4 is 1?", opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with wide-ranging applications in everyday life, finance, and various scientific fields. This article will not only answer the question directly but will also explore the underlying principles, different methods for solving percentage problems, and practical examples demonstrating the versatility of percentages. We'll delve into the concept of ratios, proportions, and even touch upon the use of calculators and spreadsheets for more complex percentage calculations.
Understanding the Fundamentals: Ratios and Proportions
Before diving into the solution, let's solidify our understanding of the core concepts involved. A percentage is simply a fraction expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, finding what percent of 4 is 1 is equivalent to finding the fraction that represents 1 out of 4, and then expressing that fraction as a percentage.
This brings us to the concept of ratios. A ratio shows the relative size of two or more values. In this case, the ratio is 1:4 (1 out of 4). We can express this ratio as a fraction: 1/4. Proportions are essentially two equal ratios. Understanding proportions is crucial for solving percentage problems, as we often set up a proportion to find the unknown percentage.
Method 1: Using a Proportion
This is a classic and highly effective method for solving percentage problems. We set up a proportion where one ratio represents the known values (1 out of 4), and the other ratio represents the unknown percentage (x out of 100).
-
Set up the proportion: 1/4 = x/100
-
Cross-multiply: To solve for x, we cross-multiply: 4x = 100
-
Solve for x: Divide both sides by 4: x = 25
Therefore, 1 is 25% of 4.
Method 2: Converting the Fraction to a Decimal and then a Percentage
This method involves expressing the ratio as a decimal first and then converting that decimal to a percentage.
-
Express as a fraction: The ratio of 1 to 4 is represented by the fraction 1/4.
-
Convert to a decimal: Divide the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25
-
Convert to a percentage: Multiply the decimal by 100: 0.25 x 100 = 25%
Again, we arrive at the same answer: 1 is 25% of 4.
Method 3: Using the Percentage Formula
The general percentage formula is: (Part / Whole) x 100 = Percentage
In this case:
- Part: 1
- Whole: 4
Substitute the values into the formula: (1 / 4) x 100 = 25%
Real-World Applications of Percentages
The ability to calculate percentages is essential in numerous real-world scenarios. Here are just a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions, from managing personal finances to analyzing investment opportunities. For example, if a store offers a 20% discount on an item, you need to calculate the discounted price.
-
Science and Statistics: Percentages are ubiquitous in scientific research and statistical analysis. Data is often expressed as percentages to represent proportions and probabilities, making it easier to compare and interpret results. Consider the success rate of a new medical treatment or the percentage of a population with a specific characteristic.
-
Everyday Life: Percentages are used in many everyday situations, such as calculating tips in restaurants, determining sale prices, understanding nutritional information on food labels (e.g., percentage of daily value of vitamins and minerals), and interpreting weather forecasts (e.g., percentage chance of rain).
-
Business and Economics: Percentages are used to track economic growth, inflation rates, unemployment rates, market share, and more. Business owners use percentages to analyze their profits, costs, and sales to make informed decisions about their operations.
Solving More Complex Percentage Problems
The methods described above can be applied to more complex percentage problems. Let's consider a few examples:
-
Finding the whole when given a part and a percentage: If 25% of a number is 5, what is the number? We can set up a proportion: 25/100 = 5/x. Solving for x, we get x = 20.
-
Finding the percentage increase or decrease: If a price increases from $10 to $12, what is the percentage increase? The increase is $2. The percentage increase is calculated as (2/10) x 100 = 20%.
-
Calculating compound interest: This involves calculating interest on both the principal and accumulated interest. Compound interest calculations use percentages repeatedly over time.
Using Technology for Percentage Calculations
For more complex problems or large datasets, technology can be a great asset. Calculators have built-in percentage functions, simplifying calculations. Spreadsheets like Microsoft Excel or Google Sheets offer powerful functions for performing percentage calculations on large datasets, such as calculating averages, sums, and variations in percentage values.
Conclusion: The Importance of Understanding Percentages
The question "What percent of 4 is 1?" may seem simple, but it underscores the importance of understanding percentages. This seemingly straightforward calculation underpins many complex mathematical operations and has practical applications in a multitude of fields. Mastering percentage calculations equips you with valuable skills applicable to personal finance, scientific analysis, business decisions, and countless other aspects of life. Whether you're using the proportion method, converting fractions to decimals, or employing the percentage formula, the ability to accurately calculate percentages is a valuable asset in today's world. The more you practice, the more confident and proficient you will become in handling percentage-related problems. Remember, understanding the underlying concepts of ratios and proportions provides a solid foundation for tackling even the most complex percentage calculations.
Latest Posts
Latest Posts
-
What Is 66 Degrees Celsius In Fahrenheit
Apr 18, 2025
-
How Many Cm Is 61 Inches
Apr 18, 2025
-
How Many Hours Is 1400 Minutes
Apr 18, 2025
-
How Do Cells Capture The Energy Released By Cellular Respiration
Apr 18, 2025
-
How Many Oz In 2 3
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 4 Is 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.