What Percent Of 40 Is 3
Kalali
Apr 25, 2025 · 5 min read
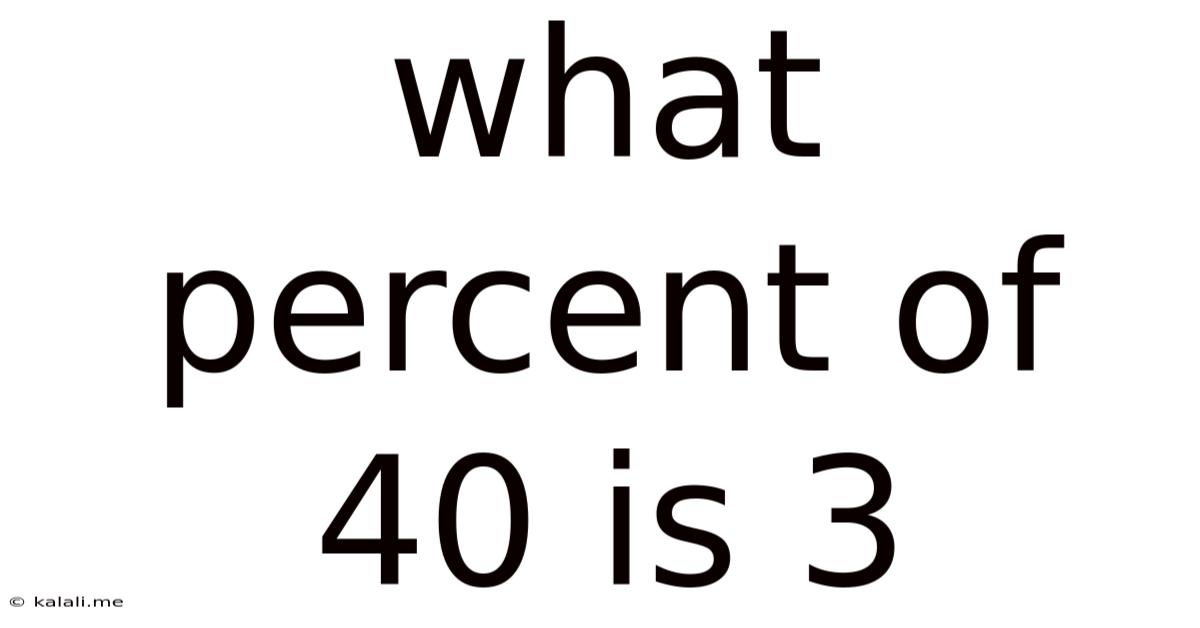
Table of Contents
What Percent of 40 is 3? Unpacking Percentages and Practical Applications
This seemingly simple question – "What percent of 40 is 3?" – opens a door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article will not only provide the answer but will also delve into the methods of calculating percentages, explore different approaches, and illustrate the relevance of percentage calculations in everyday life and professional contexts.
Meta Description: Discover how to calculate what percent of 40 is 3. This comprehensive guide explains percentage calculations, offers multiple solution methods, and explores real-world applications of percentage problems. Learn to solve similar percentage problems with ease.
Understanding Percentages: A Foundation
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for tackling percentage problems.
Percentages are used extensively to represent proportions, rates, changes, and comparisons. They're essential in finance (interest rates, discounts, taxes), statistics (data analysis), science (concentration measurements), and everyday situations (tips, sales, grades).
Method 1: Using Proportions
One of the most straightforward methods to solve "What percent of 40 is 3?" involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as a ratio:
3/40 = x/100
Where:
- 3 represents the part.
- 40 represents the whole.
- x represents the unknown percentage we are trying to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
3 * 100 = 40 * x
300 = 40x
Now, divide both sides by 40:
x = 300/40
x = 7.5
Therefore, 3 is 7.5% of 40.
Method 2: Using Decimal Conversion
Another effective method involves converting the fraction 3/40 into a decimal and then multiplying by 100 to express it as a percentage.
First, divide 3 by 40:
3 ÷ 40 = 0.075
Next, multiply the decimal by 100 to convert it to a percentage:
0.075 * 100 = 7.5%
This confirms our previous result: 3 is 7.5% of 40.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our problem:
- Part = 3
- Whole = 40
Substituting these values into the formula:
(3 / 40) * 100 = Percentage
(0.075) * 100 = 7.5%
Again, we arrive at the same answer: 3 is 7.5% of 40.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of situations. Let's explore some examples:
1. Finance:
- Interest Rates: Understanding percentage calculations is fundamental to comprehending interest rates on loans, mortgages, and savings accounts. Calculating the interest accrued on an investment or the total cost of a loan involves percentage calculations. For example, calculating simple interest on a loan requires multiplying the principal amount by the interest rate (as a decimal) and the time period.
- Discounts and Sales: Sales and discounts are often expressed as percentages. Calculating the final price of an item after a discount requires subtracting the percentage discount from the original price. For example, a 20% discount on a $50 item means a discount of $10 ($50 x 0.20), resulting in a final price of $40.
- Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages of the taxable amount. Accurately calculating taxes involves understanding percentage calculations.
- Investment Returns: Calculating the return on investment (ROI) requires determining the percentage increase or decrease in the value of an investment over a period. This helps investors evaluate the performance of their investments.
2. Statistics and Data Analysis:
- Data Representation: Percentages are used extensively in data representation to show proportions within a dataset. For example, representing survey results, demographic data, and other statistical data frequently employs percentages.
- Probability: Percentage calculations are fundamental to probability theory. Probabilities are often expressed as percentages, indicating the likelihood of an event occurring.
- Statistical Significance: In statistical hypothesis testing, percentages are used to determine the statistical significance of results.
3. Science:
- Concentration: In chemistry and other scientific disciplines, concentrations of solutions and mixtures are often expressed as percentages (e.g., percent by weight, percent by volume).
- Error Analysis: Percentage error calculations help scientists determine the accuracy and precision of experimental measurements.
4. Everyday Life:
- Tips and Gratuities: Calculating tips in restaurants or other service industries commonly involves determining a percentage of the total bill.
- Sales and Bargain Hunting: Consumers use percentage calculations to compare prices and identify the best deals while shopping.
- Grade Calculation: Students often use percentages to understand their academic performance, calculating their overall grade based on individual assignment scores.
Solving Similar Percentage Problems
The methods outlined above can be applied to solve a wide range of percentage problems. To solve any percentage problem, identify the "part," the "whole," and the unknown value. Then, use either the proportion method, decimal conversion, or the percentage formula to find the solution.
For example, let's consider another problem: "What percent of 60 is 15?"
Using the proportion method:
15/60 = x/100
1500 = 60x
x = 1500/60 = 25
Therefore, 15 is 25% of 60.
Using decimal conversion:
15 ÷ 60 = 0.25
0.25 * 100 = 25%
Using the percentage formula:
(15/60) * 100 = 25%
Conclusion
The seemingly simple question, "What percent of 40 is 3?" provides a valuable entry point into the world of percentage calculations. Understanding percentage calculations is vital for navigating various aspects of life, from personal finance and shopping to professional fields like statistics and science. By mastering the different methods outlined in this article – using proportions, decimal conversion, and the percentage formula – you'll be well-equipped to tackle a wide range of percentage problems with confidence and accuracy. Remember to practice regularly to solidify your understanding and improve your proficiency in solving percentage-related problems.
Latest Posts
Latest Posts
-
1 Percent Of 1 Million Dollars
Apr 25, 2025
-
Inverse Of 1 To 1 Function
Apr 25, 2025
-
35 Is What Percent Of 100
Apr 25, 2025
-
1 Gallon Is How Many Ml
Apr 25, 2025
-
How Do You Divide Fractions With Negative Numbers
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 40 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.