What Percent Of 40 Is 35
Kalali
Apr 11, 2025 · 5 min read
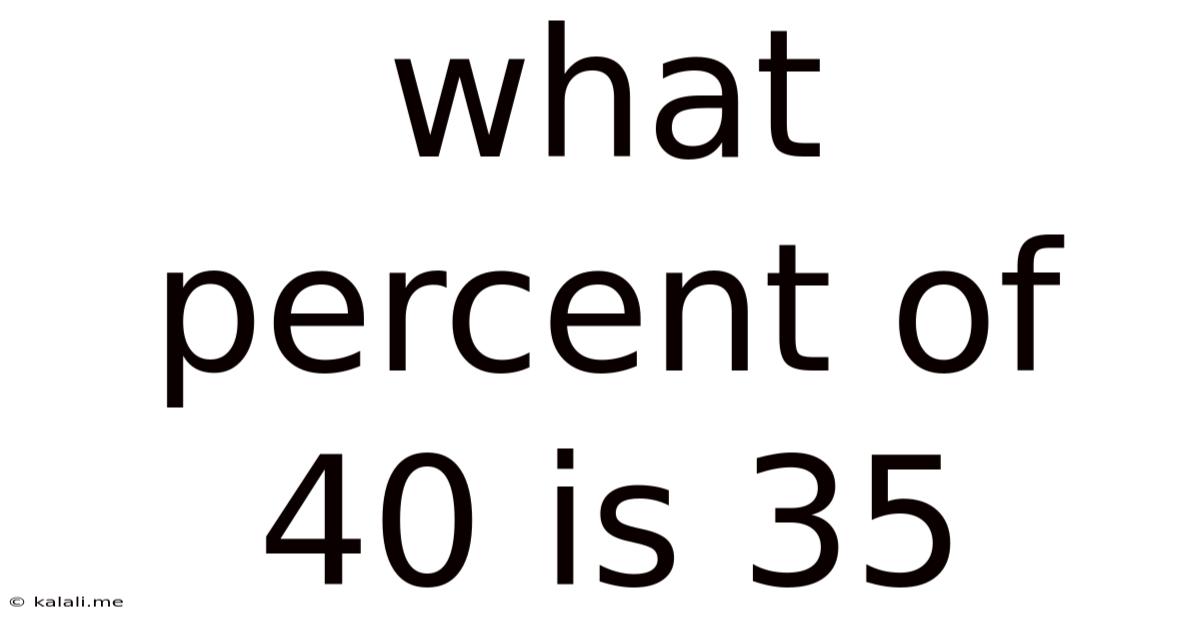
Table of Contents
What Percent of 40 is 35? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent of 40 is 35?" – opens the door to a broader understanding of percentage calculations, their applications in everyday life, and even their importance in more advanced mathematical concepts. This article will not only answer the question directly but also explore the various methods for solving percentage problems, offering a comprehensive guide for anyone looking to improve their mathematical skills. Understanding percentages is crucial for budgeting, comparing prices, calculating discounts, analyzing data, and much more.
Meta Description: Learn how to calculate percentages with a step-by-step guide answering the question: What percent of 40 is 35? This article explores various methods and real-world applications of percentage calculations.
Understanding Percentages: The Basics
Before diving into the solution, let's establish a firm grasp on the fundamental concept of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. From calculating sales tax and discounts to understanding interest rates and statistical data, percentages are an essential tool in everyday life and across numerous professional fields.
Method 1: Using Proportions to Solve "What Percent of 40 is 35?"
The most straightforward way to solve this problem is by setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
- x/100 = 35/40
Where:
- 'x' represents the unknown percentage we need to find.
- '35' is the part (the number we want to express as a percentage of 40).
- '40' is the whole (the total amount).
To solve for 'x', we can cross-multiply:
- 40x = 3500
Now, divide both sides by 40:
- x = 3500 / 40
- x = 87.5
Therefore, 35 is 87.5% of 40.
Method 2: Using the Percentage Formula
Another common approach involves using the basic percentage formula:
- Percentage = (Part / Whole) x 100
In our case:
- Part = 35
- Whole = 40
Substituting these values into the formula:
- Percentage = (35 / 40) x 100
- Percentage = 0.875 x 100
- Percentage = 87.5
Again, we arrive at the answer: 35 is 87.5% of 40.
Method 3: Deconstructing the Problem – A Step-by-Step Approach
Let's break down the problem into simpler steps for a clearer understanding:
-
Find the fraction: Express the relationship between 35 and 40 as a fraction: 35/40.
-
Simplify the fraction (optional): While not strictly necessary, simplifying the fraction can make the next step easier. We can divide both the numerator and denominator by 5: 7/8.
-
Convert the fraction to a decimal: Divide the numerator by the denominator: 7 ÷ 8 = 0.875
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.875 x 100 = 87.5%
This method highlights the underlying principles of percentage calculation, clearly illustrating the transition from fraction to decimal to percentage.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
- Finance: Calculating interest rates, loan repayments, discounts, and profit margins.
- Retail: Determining sales tax, discounts, and markups.
- Data Analysis: Representing proportions and changes in data sets, creating charts and graphs.
- Science: Expressing concentrations, probabilities, and experimental results.
- Everyday Life: Comparing prices, understanding nutritional information, and calculating tips.
Let's consider some examples:
-
Sales Discount: A store offers a 20% discount on an item priced at $50. To calculate the discount, you'd find 20% of $50 (0.20 x $50 = $10), then subtract the discount from the original price ($50 - $10 = $40).
-
Tax Calculation: A sales tax of 6% is applied to a $100 purchase. You would calculate 6% of $100 (0.06 x $100 = $6) and add it to the original price ($100 + $6 = $106).
-
Grade Calculation: If you scored 35 out of 40 on a test, your percentage score is 87.5%, as calculated earlier.
Beyond the Basics: Advanced Percentage Problems
While the problem "What percent of 40 is 35?" is relatively straightforward, percentage calculations can become more complex. Consider these examples:
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers (e.g., the percentage increase in sales from one year to the next). The formula for percentage increase is: [(New Value - Old Value) / Old Value] x 100.
-
Finding the Original Value: Determining the original price of an item after a discount has been applied (e.g., an item costs $40 after a 20% discount – what was the original price?).
-
Compound Interest: Calculating the total amount after interest is added multiple times, with each interest calculation based on the previous balance.
Mastering these advanced concepts requires a solid understanding of the fundamental principles outlined above.
Tips for Improving Your Percentage Calculation Skills
-
Practice Regularly: The best way to improve your skills is consistent practice. Try solving various percentage problems from different contexts.
-
Use Multiple Methods: Familiarize yourself with different methods of solving percentage problems (proportions, formulas, step-by-step deconstruction) to choose the most suitable approach for each problem.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Use a calculator to verify your answers, especially for more complex problems.
-
Visual Aids: Utilize diagrams, charts, or visual representations to understand percentage relationships more effectively.
-
Real-World Application: Apply percentage calculations to real-life scenarios to make the learning process more engaging and relevant.
Conclusion: The Power of Percentage Understanding
The seemingly simple question of "What percent of 40 is 35?" reveals the significance of percentage calculations in a wide range of applications. By mastering these techniques, you equip yourself with a valuable skillset applicable to numerous areas of life, from personal finance to professional endeavors. Remember, consistent practice and a clear understanding of the fundamental principles are key to mastering percentages and their diverse applications. So, next time you encounter a percentage problem, you'll be well-prepared to solve it with confidence and accuracy.
Latest Posts
Latest Posts
-
How Many Liters Is 30 Oz
Apr 18, 2025
-
How Many Cups Is In 16 9 Fl Oz Of Water
Apr 18, 2025
-
Cuanto Es Una Pulgada En Milimetros
Apr 18, 2025
-
What Is 12 16 As A Percent
Apr 18, 2025
-
What Things Are Recycled During Photosynthesis And Respiration
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 40 Is 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.