What Percent Of 5 Is 20
Kalali
Mar 08, 2025 · 4 min read
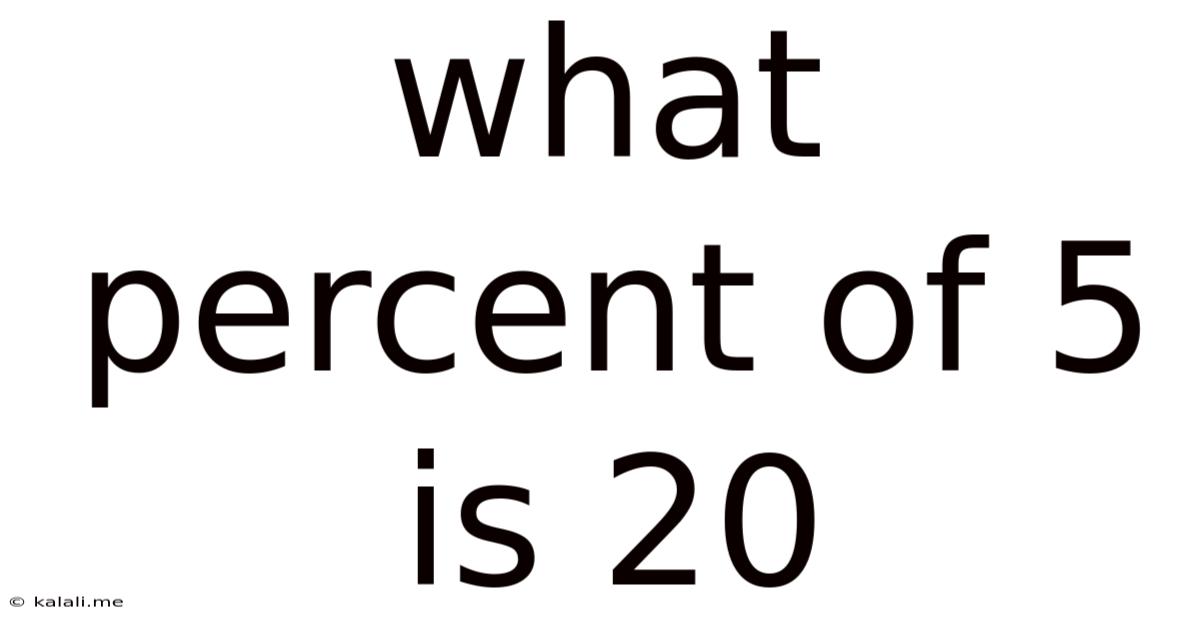
Table of Contents
What Percent of 5 is 20? Unpacking Percentages and Proportions
The question, "What percent of 5 is 20?" might seem simple at first glance, but it opens the door to understanding fundamental concepts in mathematics, particularly percentages and proportions. This seemingly straightforward query allows us to explore various methods for solving it, delve into the underlying principles, and even apply these concepts to more complex real-world scenarios. Let's unravel this mathematical puzzle step-by-step.
Understanding Percentages
Before we tackle the problem directly, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. For instance, 50% represents 50/100, which simplifies to 1/2 or 0.5. Percentages are used extensively to represent proportions, ratios, and rates of change in various fields, from finance and statistics to everyday life.
Method 1: Setting up a Proportion
One effective approach to solving "What percent of 5 is 20?" involves setting up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as follows:
- x/100 = 20/5
Here:
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (the whole).
- 20 represents the part we're interested in.
- 5 represents the whole amount.
To solve for x, we can cross-multiply:
- 5x = 2000
Then, divide both sides by 5:
- x = 400
Therefore, 20 is 400% of 5.
Method 2: Using the Percentage Formula
Another way to solve this is by using the basic percentage formula:
- Part/Whole = Percentage/100
Substituting the values from our problem:
- 20/5 = x/100
Cross-multiplying:
- 2000 = 5x
Dividing by 5:
- x = 400
Again, we arrive at the answer: 20 is 400% of 5.
Why the Result is Greater Than 100%
It's crucial to note that the result, 400%, is greater than 100%. This is perfectly valid and signifies that the "part" (20) is larger than the "whole" (5). Percentages exceeding 100% often arise when comparing a value to a smaller reference point, indicating a growth or increase beyond the initial value.
Real-World Applications: Understanding Growth and Increase
Understanding percentages exceeding 100% is vital in various real-world scenarios. Consider these examples:
- Investment Returns: If you invest $5 and your investment grows to $20, your return is 400%.
- Sales Growth: If a company's sales increase from 5 units to 20 units, it experienced a 400% growth.
- Population Increase: If a town's population grows from 5,000 to 20,000, the population increase is 400%.
In all these examples, the percentage increase significantly exceeds 100% because the final value is considerably larger than the initial value.
Method 3: Decimal Conversion and Multiplication
We can also approach this problem by first converting the percentage to a decimal. Since we're looking for what percent of 5 is 20, we can set up the equation:
- 5 * x = 20 where 'x' is the decimal equivalent of the percentage.
Solving for x:
- x = 20 / 5 = 4
Now, to convert this decimal back into a percentage, we multiply by 100:
- 4 * 100 = 400%
This method confirms our previous results.
Exploring Related Concepts: Ratios and Proportions
The problem "What percent of 5 is 20?" inherently involves ratios and proportions. A ratio is a comparison of two quantities, while a proportion is an equation stating that two ratios are equal. Understanding these concepts is fundamental in various mathematical and scientific applications.
For example, the ratio of 20 to 5 can be written as 20:5 or 20/5, which simplifies to 4:1. This ratio indicates that for every 1 unit of the whole (5), there are 4 units of the part (20). Setting up proportions allows us to solve for unknown quantities within these ratios.
Expanding the Understanding: More Complex Percentage Problems
The principles discussed here can be applied to more complex percentage problems. For example:
- Finding the original amount: If an item is increased by 20% to reach a value of $24, what was the original price? This involves working backward from the percentage increase to find the initial value.
- Calculating multiple percentage changes: If an item's price increases by 10% and then decreases by 5%, what is the overall percentage change? This involves calculating consecutive percentage changes and considering their cumulative effect.
- Percentage discounts: If an item is discounted by 25%, and its final price is $75, what was the original price? This type of problem involves using the percentage discount to find the original value.
Conclusion: Mastering Percentages and Their Applications
The simple question "What percent of 5 is 20?" provides a valuable gateway to a deeper understanding of percentages, proportions, and ratios. By exploring different methods of solving this problem, we solidify our grasp of these fundamental mathematical concepts. Furthermore, understanding percentages exceeding 100% is crucial for interpreting growth, increase, and changes in various real-world situations. Mastering these principles equips you with essential skills applicable in finance, statistics, science, and many other fields. The ability to confidently calculate and interpret percentages is a valuable asset in navigating and understanding numerical data in everyday life and professional settings. Remember that practice is key, so try solving various percentage problems to build your proficiency and confidence.
Latest Posts
Latest Posts
-
How Many Bottles Is 64 Oz Of Water
Jul 02, 2025
-
How Many Ounces In Pound Of Meat
Jul 02, 2025
-
What Is The Diameter Of A Quarter
Jul 02, 2025
-
Spoon Gets Hot In A Bowl Of Soup
Jul 02, 2025
-
How Many Cups In A 16 Oz Sour Cream
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.