What Percent Of 5 Is 3
Kalali
Mar 08, 2025 · 5 min read
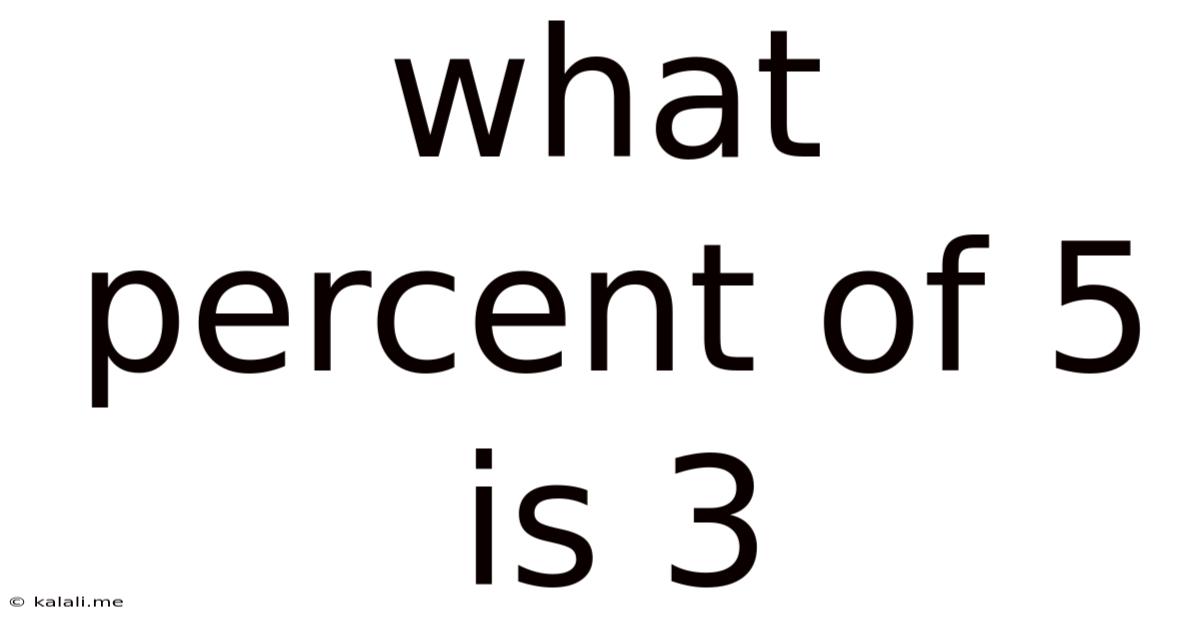
Table of Contents
What Percent of 5 is 3? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 5 is 3?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and even some advanced mathematical concepts. While the answer itself is straightforward, understanding the underlying principles allows you to confidently tackle more complex percentage problems. Let's delve into it!
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a firm grasp on the fundamental concept of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Terminology:
- Percentage: The portion represented as a number out of 100.
- Part: The specific amount we're considering (in our case, 3).
- Whole: The total amount we're considering (in our case, 5).
Calculating "What Percent of 5 is 3?"
Now, let's solve the core question. There are several ways to approach this, each offering valuable insights into percentage calculations:
Method 1: The Proportion Method
This method utilizes the concept of proportions, which are essentially two equal ratios. We can set up the proportion as follows:
x/100 = 3/5
Here:
xrepresents the unknown percentage we're trying to find.3/5represents the fraction of the whole (3 out of 5).
To solve for x, we cross-multiply:
5x = 300
Then, divide both sides by 5:
x = 60
Therefore, 3 is 60% of 5.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, we express the part (3) as a fraction of the whole (5):
3/5
Next, we convert this fraction to a decimal by dividing the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
Finally, we multiply the decimal by 100 to express it as a percentage:
0.6 x 100 = 60%
Again, we confirm that 3 is 60% of 5.
Method 3: The Formula Method
A more direct formula approach exists:
Percentage = (Part / Whole) * 100
Substituting our values:
Percentage = (3 / 5) * 100 = 0.6 * 100 = 60%
This method concisely summarizes the steps involved in the previous methods.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating interest: Banks and financial institutions utilize percentages to determine interest rates on loans and savings accounts.
- Analyzing investment returns: Investors track their investment performance using percentages to measure gains or losses.
- Budgeting and expense tracking: Individuals and businesses use percentages to allocate funds and monitor spending across various categories.
2. Sales and Discounts:
- Calculating discounts: Retailers commonly offer discounts expressed as percentages (e.g., a 20% off sale).
- Determining sale prices: Consumers calculate the final price of an item after a percentage discount.
- Analyzing sales performance: Businesses monitor their sales performance by tracking percentage changes in revenue over time.
3. Statistics and Data Analysis:
- Representing proportions: Percentages effectively represent proportions within datasets, making data easier to understand and compare.
- Calculating growth rates: Businesses and economists use percentages to calculate growth rates in various sectors, such as population growth or economic growth.
- Presenting survey results: Survey results are often expressed using percentages to represent the proportion of respondents holding specific opinions.
4. Science and Engineering:
- Expressing concentrations: In chemistry, percentages are used to express concentrations of solutions (e.g., 10% saline solution).
- Calculating efficiency: Engineers use percentages to assess the efficiency of various systems or processes.
- Analyzing experimental data: Scientists utilize percentages to analyze and interpret results from experiments and studies.
Expanding on Percentage Calculations: Advanced Concepts
While "What percent of 5 is 3?" provides a foundational understanding, let's explore some more advanced concepts:
1. Percentage Increase and Decrease:
These calculations involve finding the percentage change between two values. For instance, if a value increases from 10 to 12, the percentage increase is calculated as follows:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
In this example: [(12 - 10) / 10] * 100 = 20%
Similarly, percentage decrease is calculated using the same formula, but the result will be negative.
2. Compound Interest:
Compound interest involves calculating interest not only on the principal amount but also on accumulated interest. This leads to exponential growth over time and is a crucial concept in financial planning.
3. Percentage Points vs. Percentages:
It's crucial to understand the distinction between percentage points and percentages. A percentage point refers to the absolute difference between two percentages, while a percentage represents a relative change. For example, an increase from 10% to 15% is a 5-percentage-point increase, but a 50% relative increase (5/10 * 100).
Troubleshooting Common Percentage Calculation Mistakes
Several common mistakes can hinder accurate percentage calculations:
- Confusing the part and the whole: Always ensure you correctly identify the part and the whole before beginning the calculation.
- Incorrect decimal placement: Carefully manage decimal points during calculations to avoid errors.
- Misinterpreting percentage increase/decrease: Remember the difference between percentage points and percentage changes.
- Ignoring units: Ensure consistency in units throughout the calculation.
Conclusion: Mastering Percentages for Success
Understanding "What percent of 5 is 3?" is merely the first step in mastering percentage calculations. These calculations are fundamental to various aspects of life, from personal finance to professional endeavors. By mastering the different methods and understanding the underlying principles, you equip yourself with a valuable skill set applicable in numerous contexts. Remember to practice regularly and tackle increasingly complex problems to solidify your understanding and build confidence in tackling any percentage-related challenge that comes your way. The ability to confidently and accurately calculate percentages will undeniably enhance your problem-solving capabilities and provide a significant advantage in various aspects of life.
Latest Posts
Latest Posts
-
Why Did The Cow Want A Divorce
Jul 14, 2025
-
Lowest Common Denominator For 3 4 5
Jul 14, 2025
-
Can You Be A Professor With A Masters
Jul 14, 2025
-
How Many Bottles Of Water Is 1 Liter
Jul 14, 2025
-
How Many Days In A Million Minutes
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.