What Percent Of 50 Is 18
Kalali
Apr 07, 2025 · 5 min read
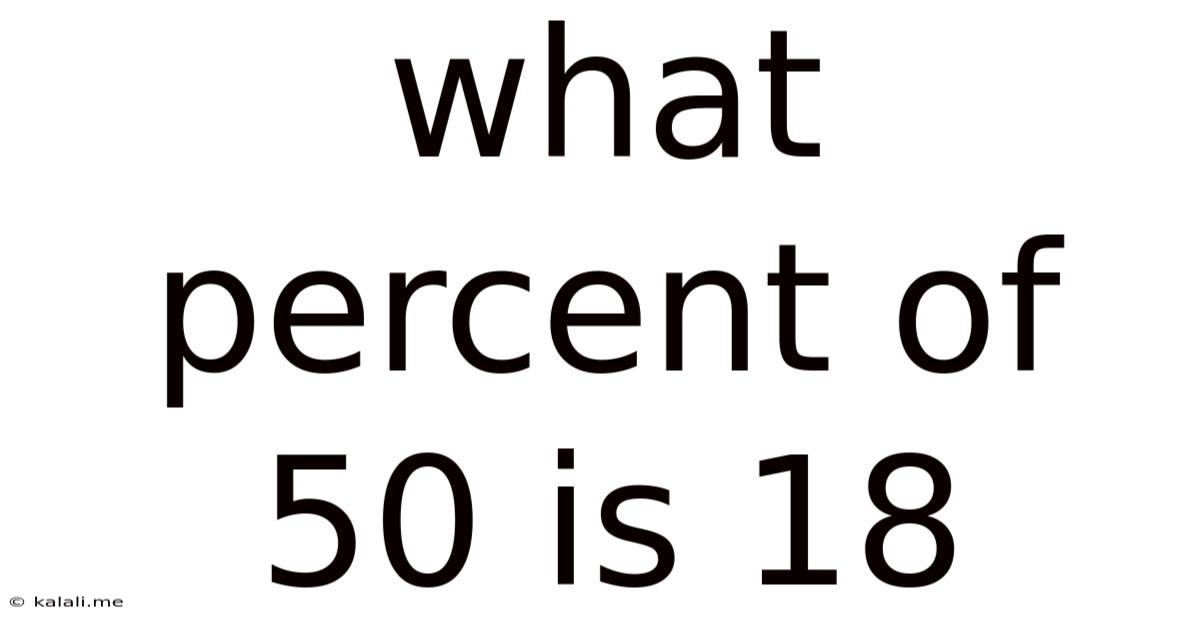
Table of Contents
- What Percent Of 50 Is 18
- Table of Contents
- What Percent of 50 is 18? A Deep Dive into Percentages and Their Applications
- Understanding Percentages: The Basics
- Calculating What Percent 18 is of 50: The Method
- Real-World Applications: Examples of Percentage Calculations
- Beyond the Basics: More Complex Percentage Problems
- Solving More Complex Percentage Problems: Step-by-Step Examples
- Practical Tips for Working with Percentages
- Conclusion: The Importance of Percentages in a Data-Driven World
- Latest Posts
- Latest Posts
- Related Post
What Percent of 50 is 18? A Deep Dive into Percentages and Their Applications
Finding what percentage a number represents of another is a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and analyzing data. This article will thoroughly explore how to determine what percent 18 is of 50, explaining the process step-by-step and providing numerous examples to illustrate its practical uses. We'll also delve into the broader context of percentages and their significance.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Percentages are used to express proportions or rates, making them a convenient way to compare and contrast different quantities. For instance, a 10% discount means that for every 100 units of price, you save 10 units.
Calculating What Percent 18 is of 50: The Method
To find what percent 18 is of 50, we employ a straightforward method:
-
Set up a ratio: Express the problem as a fraction: 18/50. This fraction represents the proportion of 18 to 50.
-
Convert the fraction to a decimal: Divide 18 by 50: 18 ÷ 50 = 0.36
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.36 x 100 = 36%
Therefore, 18 is 36% of 50.
Real-World Applications: Examples of Percentage Calculations
Percentages are ubiquitous in our daily lives. Here are some examples demonstrating their practical applications:
-
Discounts and Sales: A store offers a 20% discount on an item originally priced at $100. To calculate the discount, we find 20% of $100: (20/100) x $100 = $20. The sale price is $100 - $20 = $80.
-
Taxes: A 6% sales tax is levied on a purchase of $50. The tax amount is (6/100) x $50 = $3. The total cost is $50 + $3 = $53.
-
Grade Calculations: A student scores 45 out of 60 points on a test. To calculate the percentage score, we find (45/60) x 100 = 75%.
-
Interest Rates: A savings account earns 3% annual interest on a balance of $2000. The interest earned in one year is (3/100) x $2000 = $60.
-
Surveys and Polls: In a survey of 200 people, 80 people prefer a certain brand of soda. The percentage of people who prefer that brand is (80/200) x 100 = 40%.
-
Data Analysis: Percentages are extensively used to represent data in various fields like finance, economics, and healthcare. For instance, comparing growth rates of companies, analyzing market share, or showing disease prevalence.
-
Tip Calculation: You want to leave a 15% tip on a restaurant bill of $75. The tip amount is (15/100) x $75 = $11.25.
Beyond the Basics: More Complex Percentage Problems
While the example of finding what percent 18 is of 50 is relatively straightforward, more complex percentage problems can arise. These might involve:
-
Finding the original value: If an item is discounted by 25% and the sale price is $60, what was the original price? This requires working backward from the percentage and sale price.
-
Calculating percentage increase or decrease: If a quantity increases from 50 to 65, what is the percentage increase? This involves calculating the difference, dividing it by the original value, and then multiplying by 100.
-
Compound percentages: These involve applying percentages successively, as seen in compound interest calculations, where interest earned is added to the principal amount, and subsequent interest is calculated on this larger amount.
Solving More Complex Percentage Problems: Step-by-Step Examples
Example 1: Finding the Original Price
A jacket is on sale for $75 after a 20% discount. What was the original price?
-
Let x be the original price.
-
Express the discount as a decimal: 20% = 0.20
-
Set up an equation: x - 0.20x = $75 (This represents the original price minus the discount equals the sale price)
-
Simplify and solve for x: 0.80x = $75 => x = $75 / 0.80 = $93.75
The original price of the jacket was $93.75.
Example 2: Calculating Percentage Increase
The number of students enrolled in a school increased from 500 to 600. What is the percentage increase?
-
Calculate the difference: 600 - 500 = 100
-
Divide the difference by the original value: 100 / 500 = 0.20
-
Multiply by 100 to convert to a percentage: 0.20 x 100 = 20%
The percentage increase in student enrollment is 20%.
Practical Tips for Working with Percentages
-
Master the fundamentals: Thoroughly understand the basic concepts of fractions, decimals, and ratios, as these are essential for working with percentages.
-
Use a calculator: While simpler percentage problems can be solved manually, a calculator is helpful for more complex calculations.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Practice regularly: The more you practice solving percentage problems, the more proficient you'll become.
-
Understand the context: Always pay attention to the context of the problem to ensure you're applying the correct method.
Conclusion: The Importance of Percentages in a Data-Driven World
Percentages are an indispensable tool for understanding and communicating quantitative information. Their versatility makes them valuable across numerous disciplines, from everyday personal finance to complex statistical analysis. Mastering the art of percentage calculations is not just a valuable mathematical skill but a crucial life skill in navigating our increasingly data-driven world. By understanding the principles outlined in this article, you can confidently tackle a wide range of percentage problems and apply this knowledge to various real-world scenarios. Remember to practice regularly and always double-check your calculations to ensure accuracy.
Latest Posts
Latest Posts
-
What Is The Relationship Between Mistletoe And Spruce
Apr 10, 2025
-
How Many Square Feet In One Yard
Apr 10, 2025
-
14 Hours Is How Many Minutes
Apr 10, 2025
-
How Many Meters Is 30 Yards
Apr 10, 2025
-
How Many Inches Are In 4 Meters
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.