What Percent Of 50 Is 36
Kalali
Apr 26, 2025 · 5 min read
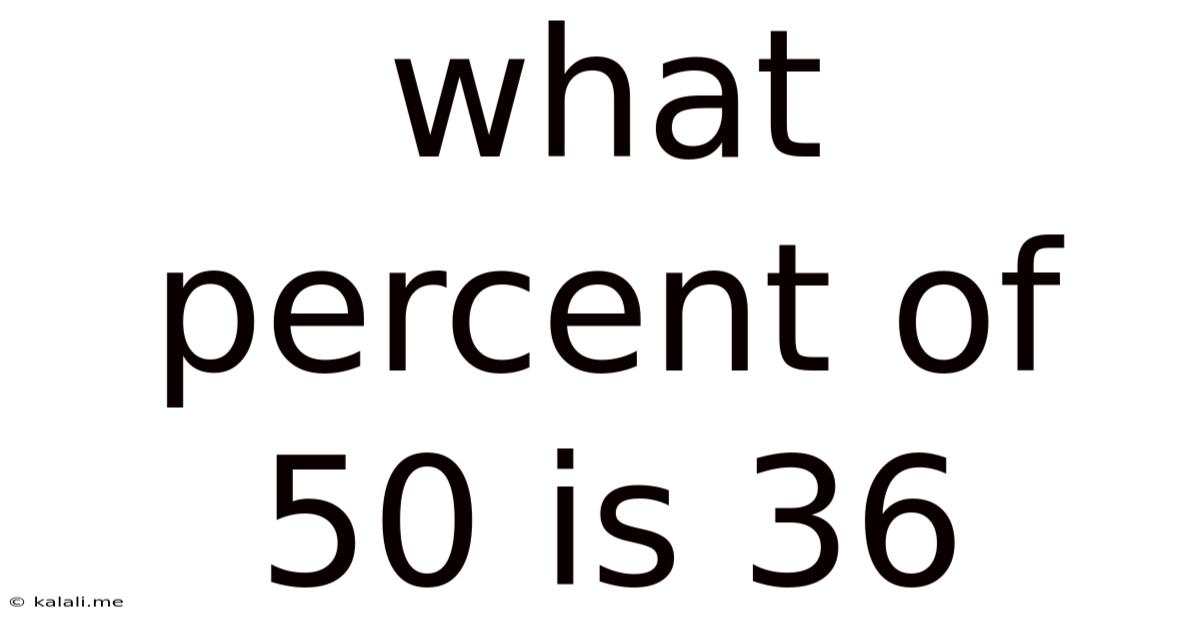
Table of Contents
What Percent of 50 is 36? A Deep Dive into Percentage Calculations and Applications
Finding what percentage 36 represents of 50 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept with widespread applications across numerous fields. This article will not only answer the question directly but also delve into the underlying mathematics, explore various methods of calculation, and showcase real-world examples where this type of percentage calculation is crucial. We'll examine different approaches, from basic arithmetic to using proportions and even employing algebraic equations, solidifying your grasp of percentages and their practical uses.
Understanding Percentages: A Foundational Concept
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred." When we say "x% of y," we're asking what fraction of y is equal to x, scaled to a denominator of 100. This seemingly simple concept forms the bedrock of countless calculations in finance, statistics, science, and everyday life. Understanding percentages allows us to compare quantities, analyze data, and make informed decisions.
Method 1: The Direct Arithmetic Approach
The most straightforward method to determine what percentage 36 is of 50 is through direct arithmetic. The process involves the following steps:
-
Formulate the fraction: Express the relationship between 36 and 50 as a fraction: 36/50.
-
Convert to decimal: Divide the numerator (36) by the denominator (50): 36 ÷ 50 = 0.72.
-
Convert to percentage: Multiply the decimal by 100 to express it as a percentage: 0.72 x 100 = 72%.
Therefore, 36 is 72% of 50.
Method 2: Using Proportions
Proportions offer a more elegant and versatile approach to solving percentage problems. A proportion sets up an equivalence between two ratios. In this case, we can set up the following proportion:
36/50 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
50x = 3600
Then, divide both sides by 50:
x = 3600 ÷ 50 = 72
Again, we find that 36 is 72% of 50. The beauty of this method lies in its adaptability to various percentage problems, even those with unknown quantities other than the percentage itself.
Method 3: Algebraic Equation
We can also approach this problem using an algebraic equation. Let's represent the unknown percentage as 'p'. The problem can be written as:
p/100 * 50 = 36
To solve for 'p', we first simplify the equation:
50p/100 = 36
Then, multiply both sides by 100:
50p = 3600
Finally, divide both sides by 50:
p = 72
This confirms once more that 36 is 72% of 50. This method emphasizes the underlying mathematical relationship and reinforces the understanding of percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a highly valuable skill with applications across a broad spectrum of fields:
1. Finance and Business:
-
Profit margins: Businesses use percentage calculations to determine their profit margin – the percentage of revenue remaining after deducting costs. Understanding profit margins is crucial for pricing strategies, assessing financial health, and making informed business decisions. For example, if a company has a cost of goods sold of $34 and sells a product for $50, its profit margin is calculated as (50-34)/50 * 100 = 32%. Similar calculations are used for analyzing gross profit, net profit, and return on investment (ROI).
-
Interest rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Accurately calculating interest payments or accrued interest requires a solid grasp of percentage calculations. Compound interest calculations rely heavily on percentage computations over multiple periods.
-
Discounts and sales: Retailers frequently offer discounts expressed as percentages. Calculating the final price after a discount requires determining the percentage reduction and applying it to the original price. For example, a 20% discount on a $50 item results in a price reduction of 0.20 * $50 = $10, resulting in a final price of $40.
2. Science and Statistics:
-
Data analysis: Percentages are fundamental to presenting and interpreting statistical data. Researchers use percentages to express proportions, probabilities, and changes in variables. For instance, in clinical trials, the success rate of a treatment might be expressed as a percentage.
-
Scientific measurements: Many scientific measurements involve percentages, such as concentration of solutions, error margins in experiments, and changes in various physical properties.
-
Population studies: Demographers use percentages to represent population growth, decline, and the distribution of various characteristics within a population.
3. Everyday Life:
-
Tip calculations: Calculating tips in restaurants or for service providers typically involves determining a percentage of the total bill.
-
Tax calculations: Sales tax, income tax, and other taxes are frequently expressed as percentages of the taxable amount.
-
Grading systems: Many educational institutions use percentage-based grading systems to evaluate student performance. Understanding percentages is crucial for students to track their academic progress and understand their grades.
Advanced Percentage Calculations
While the example of finding what percentage 36 is of 50 demonstrates basic percentage calculations, more complex scenarios require advanced techniques:
-
Finding the original value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 72% of a number is 36, the original number can be calculated as 36 / 0.72 = 50.
-
Percentage change: Calculating the percentage increase or decrease between two values involves finding the difference between the values, dividing by the original value, and multiplying by 100. This is crucial for tracking changes over time in various metrics like sales figures, stock prices, or population sizes.
-
Compounding percentages: When percentages are applied repeatedly (like compound interest), the calculations become more complex, requiring the use of exponential functions or iterative methods.
Conclusion
Determining that 36 is 72% of 50 is just the tip of the iceberg when it comes to understanding and applying percentage calculations. This fundamental concept underpins countless calculations in diverse fields, from finance and business to science and everyday life. Mastering various methods for calculating percentages – whether through direct arithmetic, proportions, or algebraic equations – equips you with a valuable skill set that enhances your analytical abilities and enables you to make informed decisions across numerous contexts. The ability to confidently manipulate and interpret percentages is a key component of both numerical literacy and effective problem-solving. By understanding the underlying principles and practicing different approaches, you can confidently tackle a wide range of percentage-related problems and effectively apply this crucial skill in your personal and professional life.
Latest Posts
Latest Posts
-
What Percent Is 11 Out Of 18
Apr 26, 2025
-
How Many Centimeters In 50 Meters
Apr 26, 2025
-
4 Liters Is Equal To How Many Gallons
Apr 26, 2025
-
What Temperature Is 180 Celsius In Fahrenheit
Apr 26, 2025
-
How Does The Altitude Affect Climate
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.