What Percent Of 6 Is 2
Kalali
Apr 17, 2025 · 4 min read
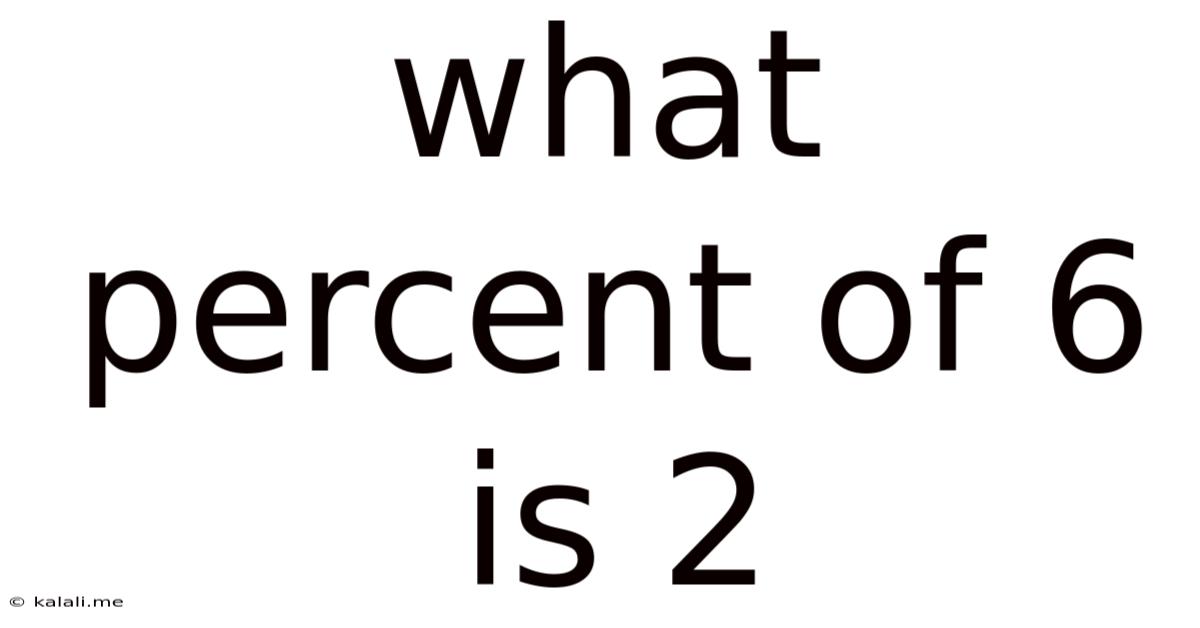
Table of Contents
What Percent of 6 is 2? A Deep Dive into Percentage Calculations
What percent of 6 is 2? This seemingly simple question opens the door to a broader understanding of percentage calculations, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial data. This article will not only answer the initial question but also explore the various methods for solving percentage problems, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (from the Latin per centum). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental relationship is key to mastering percentage calculations.
Method 1: Using Proportions to Solve "What Percent of 6 is 2?"
This method utilizes the power of proportions – equating two ratios to find an unknown value. We can set up a proportion as follows:
- Part / Whole = Percentage / 100
In our problem, "What percent of 6 is 2?", we know:
- Part: 2 (the number we're considering as a part of the whole)
- Whole: 6 (the total amount)
- Percentage: x (this is what we need to find)
Substituting these values into our proportion, we get:
2 / 6 = x / 100
To solve for x, we cross-multiply:
2 * 100 = 6 * x
200 = 6x
Now, divide both sides by 6:
x = 200 / 6 = 33.333...
Therefore, 2 is approximately 33.33% of 6.
Method 2: Using the Percentage Formula
The percentage formula provides a more direct approach:
- Percentage = (Part / Whole) * 100
Again, using our values:
- Part: 2
- Whole: 6
Plugging these into the formula:
Percentage = (2 / 6) * 100
Percentage = 0.3333... * 100
Percentage ≈ 33.33%
This method yields the same result as the proportion method, confirming our answer.
Method 3: Decimal Conversion and Multiplication
This method involves converting the fraction to a decimal and then multiplying by 100.
First, express the relationship as a fraction: 2/6
Simplify the fraction: 1/3
Convert the fraction to a decimal: 1 ÷ 3 ≈ 0.3333
Multiply the decimal by 100 to express it as a percentage: 0.3333 * 100 ≈ 33.33%
Understanding Recurring Decimals and Rounding
Notice that in our calculations, we encountered a recurring decimal (0.333...). This is because 1/3 is a fraction that cannot be expressed exactly as a terminating decimal. In practical applications, we often round these decimals to a certain number of decimal places – in this case, we rounded to two decimal places (33.33%). The level of precision required depends on the context of the problem. For instance, in financial calculations, higher precision might be necessary.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of our lives:
-
Discounts and Sales: Stores frequently advertise discounts like "20% off." Understanding percentages allows you to quickly calculate the actual savings.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages.
-
Financial Analysis: Percentages are crucial for analyzing financial statements, calculating interest rates, and understanding investment returns. Understanding percentage change (increase or decrease) is essential for tracking performance.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions in data sets, making it easier to understand trends and patterns. For example, understanding the percentage of a population that holds a certain opinion is crucial for market research.
-
Grade Calculations: Academic grades are often expressed as percentages, reflecting the proportion of correct answers or the overall performance in a course.
Advanced Percentage Problems and Solving Techniques
Beyond the basic "what percent of X is Y" problems, there are more complex percentage scenarios:
-
Finding the Whole: If you know the percentage and the part, you can solve for the whole. For example: "15% of what number is 3?"
-
Finding the Part: If you know the percentage and the whole, you can solve for the part. For example: "What is 25% of 80?"
-
Percentage Increase/Decrease: These calculations involve determining the percentage change between two values. For example, if a price increases from $10 to $12, what is the percentage increase?
-
Compound Interest: This involves calculating interest on both the principal and accumulated interest over time.
Solving More Complex Problems
Let's tackle a slightly more complex example: "If a store offers a 20% discount on an item priced at $50, what is the final price?"
-
Calculate the discount amount: 20% of $50 is (20/100) * $50 = $10
-
Subtract the discount from the original price: $50 - $10 = $40
Therefore, the final price after the 20% discount is $40.
Conclusion: Mastering Percentages for Everyday Success
Understanding percentages is a fundamental skill with far-reaching applications. From simple calculations like "What percent of 6 is 2?" to more complex financial and statistical analyses, the ability to work with percentages is essential for navigating the numerical aspects of everyday life and achieving success in various fields. By mastering the different methods outlined in this article and practicing with various problem types, you can build a strong foundation in percentage calculations and confidently tackle any percentage-related challenge you encounter. Remember to always check your work and consider the context of the problem to ensure your answer is both accurate and relevant.
Latest Posts
Latest Posts
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
-
What Is 6 Ft 1 In Cm
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 6 Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.