What Percent Of 6 Is 5
Kalali
Mar 11, 2025 · 4 min read
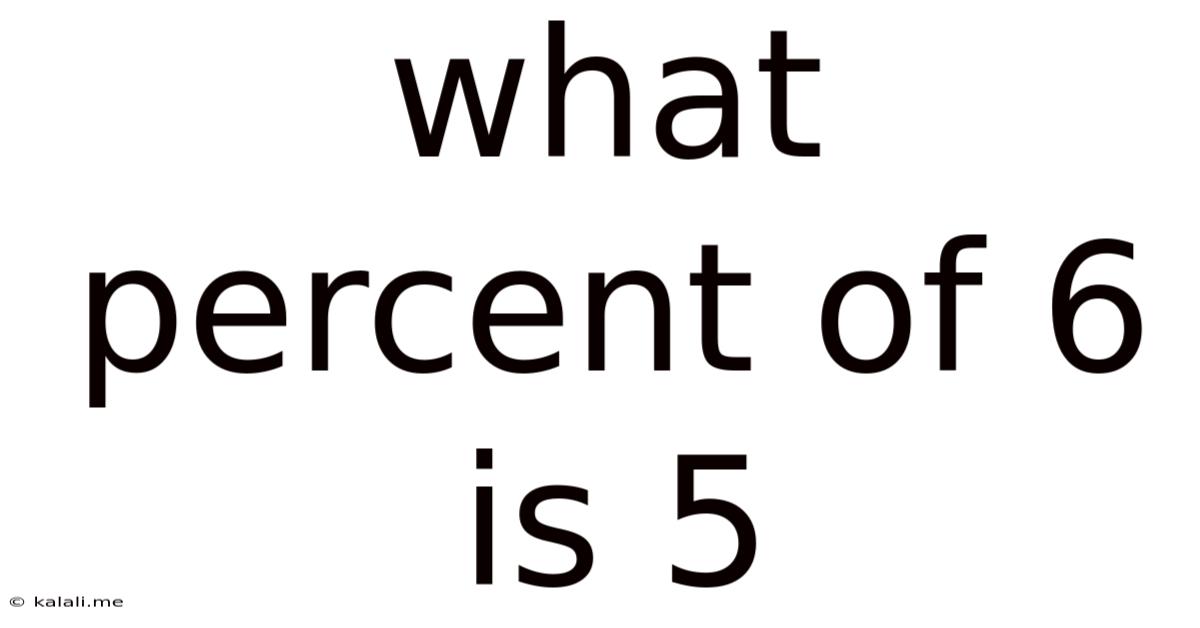
Table of Contents
What Percent of 6 is 5? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 6 is 5?", opens the door to a fascinating exploration of percentage calculations, their applications, and their importance in various fields. While the answer itself is straightforward, understanding the underlying principles empowers you to tackle more complex percentage problems with confidence. This comprehensive guide will not only provide the solution but also delve into the methodology, practical examples, and related concepts.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. It represents a proportion of a whole. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Percentages are ubiquitous in everyday life, appearing in sales discounts, interest rates, statistical data, and much more.
Calculating "What Percent of 6 is 5?"
To find what percent of 6 is 5, we can use a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 5 (the value we're considering as a part of the whole)
- Whole: 6 (the total value)
Let's plug these values into the formula:
(5 / 6) * 100% = 83.33% (approximately)
Therefore, 5 is approximately 83.33% of 6.
Different Approaches to Solving Percentage Problems
While the above method is the most straightforward, there are other ways to approach this problem, each offering valuable insights into percentage calculations:
Method 2: Using Proportions
We can set up a proportion to solve the problem:
5/6 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
6x = 500
x = 500/6
x ≈ 83.33
This confirms our previous result.
Method 3: Working with Decimals
We can convert the fraction 5/6 to a decimal by performing the division:
5 ÷ 6 ≈ 0.8333
Then, to express this decimal as a percentage, we multiply by 100%:
0.8333 * 100% ≈ 83.33%
Real-World Applications of Percentage Calculations
Percentage calculations are essential across diverse fields. Here are some examples:
Finance and Investment
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Returns on Investment (ROI): Investors use percentages to measure the profitability of their investments.
- Discounts and Sales Tax: Businesses utilize percentages to offer discounts and calculate sales tax on purchases.
Science and Statistics
- Data Analysis: Percentages are crucial for representing and interpreting statistical data, such as population demographics or survey results.
- Scientific Experiments: Percentages are used to express the yield of a chemical reaction or the success rate of a clinical trial.
Everyday Life
- Tip Calculations: People use percentages to calculate tips in restaurants.
- Grocery Shopping: Understanding unit prices and discounts often requires percentage calculations.
- Cooking and Baking: Recipes sometimes specify ingredients as percentages of the total weight or volume.
Advanced Percentage Problems and Concepts
While the initial problem was relatively simple, the world of percentages extends to more complex scenarios:
Finding the Whole when the Percentage and Part are Known
Imagine a scenario where you know that 20% of a certain number is 10. To find the whole number, you can use the following formula:
(Part / Percentage) * 100 = Whole
(10 / 20) * 100 = 50
Therefore, the whole number is 50.
Finding the Part when the Percentage and Whole are Known
Suppose you want to find 30% of 200. The calculation is:
(Percentage / 100) * Whole = Part
(30 / 100) * 200 = 60
Percentage Increase and Decrease
Calculating percentage increases and decreases is common in various contexts:
- Percentage Increase: [(New Value - Old Value) / Old Value] * 100%
- Percentage Decrease: [(Old Value - New Value) / Old Value] * 100%
For example, if a price increases from $100 to $120, the percentage increase is:
[(120 - 100) / 100] * 100% = 20%
Mastering Percentages: Tips and Tricks
To become proficient in percentage calculations:
- Practice Regularly: Consistent practice is key to mastering any mathematical concept.
- Understand the Formula: A clear grasp of the basic percentage formula is essential.
- Use Different Methods: Experiment with various approaches to solving percentage problems.
- Visual Aids: Diagrams and charts can be helpful for visualizing percentages.
- Check Your Work: Always verify your answers to ensure accuracy.
Conclusion: The Power of Percentages
This in-depth look at the seemingly simple question, "What percent of 6 is 5?", reveals the wide-ranging applications and significance of percentage calculations. From financial transactions to scientific research and everyday life, percentages provide a powerful tool for understanding proportions and making informed decisions. By mastering the fundamental principles and exploring various calculation methods, you can confidently tackle a wide array of percentage-related problems and unlock a deeper understanding of the world around you. Remember to practice regularly and explore different approaches to solidify your understanding and build your problem-solving skills. The more you work with percentages, the more intuitive and effortless the calculations will become.
Latest Posts
Latest Posts
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
-
How Many Centimeters Are In A Meter Stick
Jul 10, 2025
-
Why Did The Orchestra Get An R Rating
Jul 10, 2025
-
Is 27 A Prime Or Composite Number
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 6 Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.