What Percent Of 60 Is 150
Kalali
Apr 23, 2025 · 4 min read
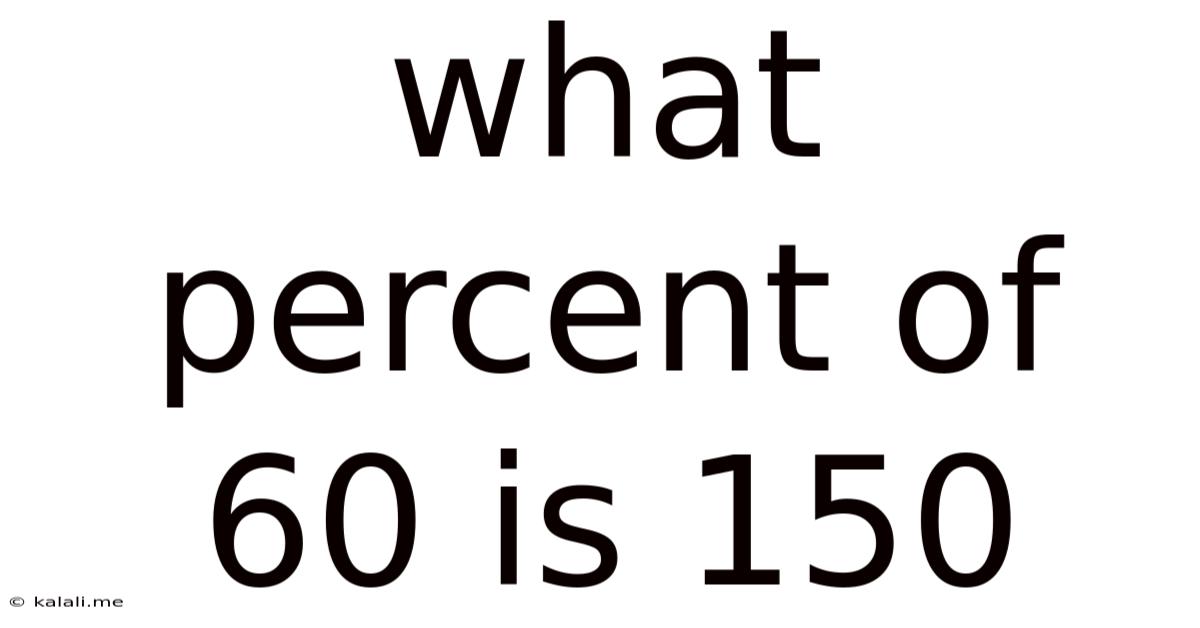
Table of Contents
What Percent of 60 is 150? Unraveling Percentages and Proportions
This seemingly simple question, "What percent of 60 is 150?", opens the door to a deeper understanding of percentages, proportions, and their applications in everyday life. While the answer might seem counterintuitive at first glance (since 150 is larger than 60), understanding the underlying mathematical principles reveals a clear and straightforward solution. This article will not only provide the answer but also delve into the methods used to solve it, explore related concepts, and demonstrate practical applications. We'll also touch upon how to confidently tackle similar percentage problems.
Understanding the Problem: Deconstructing the Question
The core of the question lies in understanding the relationship between a part (150) and a whole (60). Traditionally, we think of percentages as representing a fraction of 100. However, this problem presents a scenario where the "part" is larger than the "whole." This doesn't invalidate the concept; it simply means the percentage will be greater than 100%. This signifies that 150 represents more than the entirety of 60; it’s a multiple of 60.
Method 1: Using the Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 150
- Whole: 60
Substituting these values into the formula:
(150 / 60) * 100% = 250%
Therefore, 150 is 250% of 60.
Method 2: Proportions and Cross-Multiplication
Percentage problems can also be solved using proportions. We can set up a proportion to represent the relationship between the parts and the whole:
150/60 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
150 * 100 = 60 * x
15000 = 60x
x = 15000 / 60
x = 250
Again, we find that 150 is 250% of 60.
Method 3: Finding the Multiplier
A more intuitive approach involves finding how many times 60 goes into 150. We can simply divide 150 by 60:
150 / 60 = 2.5
This tells us that 150 is 2.5 times larger than 60. To express this as a percentage, we multiply by 100%:
2.5 * 100% = 250%
Interpreting the Result: What Does 250% Mean?
The result, 250%, indicates that 150 is two and a half times the size of 60. It's crucial to understand that percentages exceeding 100% are perfectly valid and represent quantities greater than the whole. In this context, it signifies a significant increase or growth relative to the original value of 60.
Practical Applications of Percentages Greater Than 100%
Percentages exceeding 100% frequently appear in various real-world scenarios:
- Financial Growth: If a company's revenue increased from $60 million to $150 million, the growth would be calculated as 250%.
- Population Increase: If a town's population grew from 60,000 to 150,000, the population increase would be 250%.
- Sales Increases: If a business’s sales increased from 60 units to 150 units, that is a 250% increase.
- Inflation: If the price of a product increased from $60 to $150, the inflation is 250%.
- Investment Returns: If an investment of $60 generated a return of $150, the return on investment would be 250%.
Further Exploration: Related Percentage Problems
Mastering the concept of percentages extends beyond this specific problem. Let's explore some related scenarios and how to solve them:
- Finding the Part: "What is 250% of 60?" This is a straightforward calculation: (250/100) * 60 = 150.
- Finding the Whole: "150 is 250% of what number?" This requires rearranging the percentage formula: (150 / 2.5) = 60.
- Percentage Decrease: If a value decreases from 150 to 60, the percentage decrease is calculated as: ((150 - 60) / 150) * 100% = 60%. This demonstrates that percentage changes can be both positive (increases) and negative (decreases).
- Compound Percentages: When dealing with multiple percentage changes, we need to account for compounding. For instance, if a value increases by 50% and then decreases by 50%, the final value is not the original value. It will be less, because the 50% decrease is calculated from the increased value, not the original value.
Advanced Applications and Considerations
Understanding percentages and their applications is fundamental to various fields, including:
- Finance: Calculating interest rates, returns on investments, inflation rates, and more.
- Statistics: Analyzing data, calculating probabilities, and interpreting statistical significance.
- Business: Analyzing sales figures, market share, and profitability.
- Science: Expressing experimental results, calculating error margins, and analyzing data.
Conclusion: Mastering Percentages for Real-World Success
The question, "What percent of 60 is 150?", serves as a springboard for exploring the versatile world of percentages. By understanding the underlying principles, applying the correct formulas, and interpreting the results accurately, you can confidently tackle a wide range of percentage problems. Remember that percentages exceeding 100% are entirely valid and frequently encountered in real-world situations. The ability to confidently work with percentages is a valuable skill that enhances your analytical abilities and problem-solving capabilities across numerous disciplines. Practice makes perfect, so continue practicing different percentage problems to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
What Factors Affect The Rate Of Thermal Energy Transfer
Apr 24, 2025
-
How Many Feet Is 105 Cm
Apr 24, 2025
-
How Many Inches In 78 Cm
Apr 24, 2025
-
Cuanto Es 14 Metros En Pies
Apr 24, 2025
-
How Many Cups Are In 20 Fluid Ounces
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.