What Percent Of 60 Is 20
Kalali
Apr 17, 2025 · 5 min read
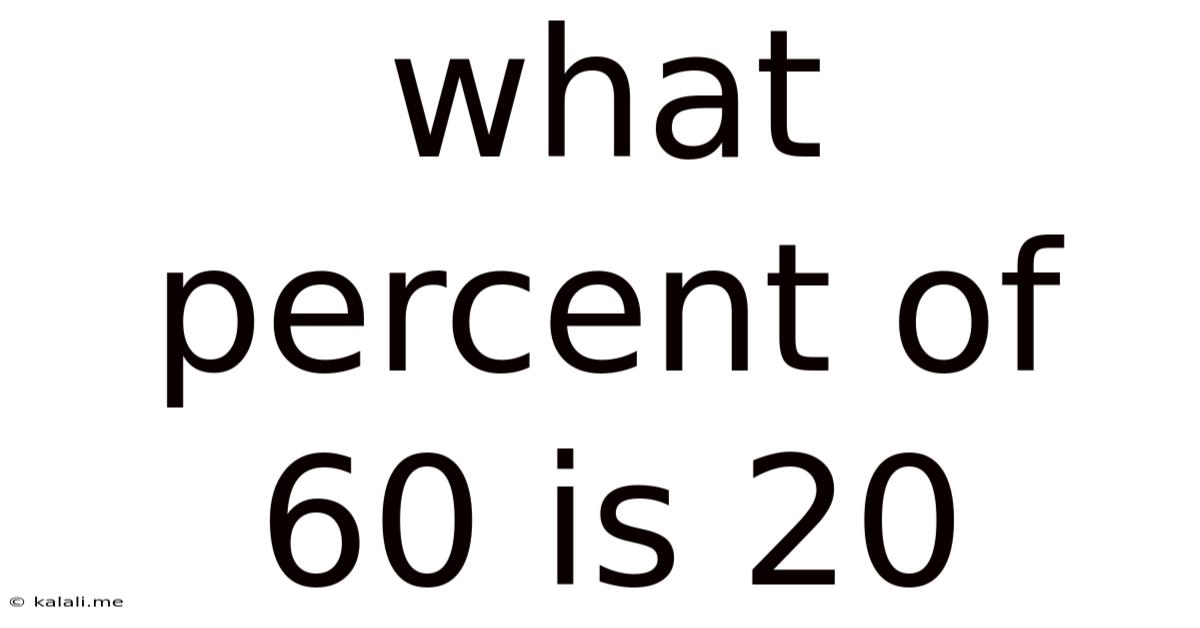
Table of Contents
What Percent of 60 is 20? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "What percent of 60 is 20?" – opens the door to a broader understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will not only answer the question directly but also delve into the underlying principles, explore different calculation methods, and provide real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to find what percent of 60 is 20, covering various methods and real-world applications. Master percentage calculations today!
Understanding Percentages
Before diving into the calculation, let's establish a firm grasp of what percentages represent. A percentage is a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." Therefore, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Percentages are used to represent proportions or ratios. They provide a standardized way to compare different quantities, making it easier to understand relative sizes and changes. For instance, if a store offers a 20% discount, it means you'll pay 80% (100% - 20%) of the original price.
Method 1: Using the Formula
The most straightforward method to determine what percent of 60 is 20 involves using a simple percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 20 (the number we're comparing)
- Whole: 60 (the total number)
Substituting these values into the formula:
(20 / 60) * 100% = 33.33%
Therefore, 20 is approximately 33.33% of 60. The slight rounding is due to the recurring decimal in the result.
Method 2: Setting Up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
20/60 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
20 * 100 = 60 * x
2000 = 60x
x = 2000 / 60
x = 33.33%
This method confirms our previous result: 20 is approximately 33.33% of 60.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, express the ratio as a fraction: 20/60
Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 20:
20/60 = 1/3
Now, convert the fraction to a decimal by dividing the numerator by the denominator:
1 ÷ 3 ≈ 0.3333
Finally, multiply the decimal by 100% to express it as a percentage:
0.3333 * 100% ≈ 33.33%
Again, we arrive at the same answer. This method highlights the interchangeable nature of fractions, decimals, and percentages.
Real-World Applications
Understanding percentage calculations is crucial in numerous everyday situations:
-
Shopping Discounts: Imagine a shirt originally priced at $60 is on sale for $20 off. Using the methods above, you'd quickly determine that the discount is 33.33%.
-
Tax Calculations: If a sales tax is 6% and you purchase an item for $60, calculating the tax amount involves finding 6% of $60. This is a vital skill for budgeting and managing finances.
-
Grade Calculation: If you scored 20 points out of a possible 60 on a test, your percentage score would be 33.33%, providing a clear understanding of your performance.
-
Financial Analysis: Investors and financial analysts frequently use percentages to analyze market trends, assess investment returns, and compare the performance of different assets. Understanding percentage changes is key to interpreting financial data.
-
Data Interpretation: Percentages are crucial for interpreting statistical data. For example, understanding the percentage change in unemployment rates or the percentage of voters supporting a particular candidate helps in comprehending complex information.
Beyond the Basics: Dealing with More Complex Scenarios
While the example of "What percent of 60 is 20?" provides a clear introduction, percentage calculations can become more complex. Here are some variations:
-
Finding the Whole: If you know a percentage and the part, you can determine the whole. For example, if 33.33% of a number is 20, you can use the formula: (Part / Percentage) * 100 = Whole.
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example, to find 33.33% of 60, you would multiply 60 by 0.3333.
-
Percentage Increase/Decrease: These calculations involve finding the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%.
-
Compound Percentage: This type of calculation involves applying a percentage change repeatedly over time. It's often used in financial calculations involving interest rates.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Work through various examples, including those with different levels of complexity.
-
Use a Calculator: While understanding the underlying principles is vital, using a calculator can save time, especially when dealing with more complex calculations or recurring decimals.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, manageable steps. This will make the process less daunting and less prone to errors.
-
Check Your Work: Always double-check your calculations to ensure accuracy. A simple mistake can significantly alter the result.
-
Understand the Context: Pay close attention to the context of the problem. Understanding what the numbers represent will help you determine the appropriate calculation method.
Conclusion: The Power of Percentage Understanding
The seemingly simple question of "What percent of 60 is 20?" unveils the power and versatility of percentage calculations. Mastering these calculations equips you with a valuable skill applicable in various aspects of life, from personal finance to professional pursuits. By understanding the different calculation methods and practicing regularly, you can confidently tackle any percentage-related problem and make informed decisions based on accurate data. Remember, percentages are more than just numbers; they're a powerful tool for interpreting and understanding the world around us.
Latest Posts
Latest Posts
-
What Is 98 Inches In Feet
Apr 19, 2025
-
How Many Cups Are In 20oz
Apr 19, 2025
-
How Many Diagonals Has A Hexagon
Apr 19, 2025
-
9 As A Percentage Of 25
Apr 19, 2025
-
What Is 1 12 In A Decimal
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.