What Percent Of 72 Is 27
Kalali
Apr 25, 2025 · 4 min read
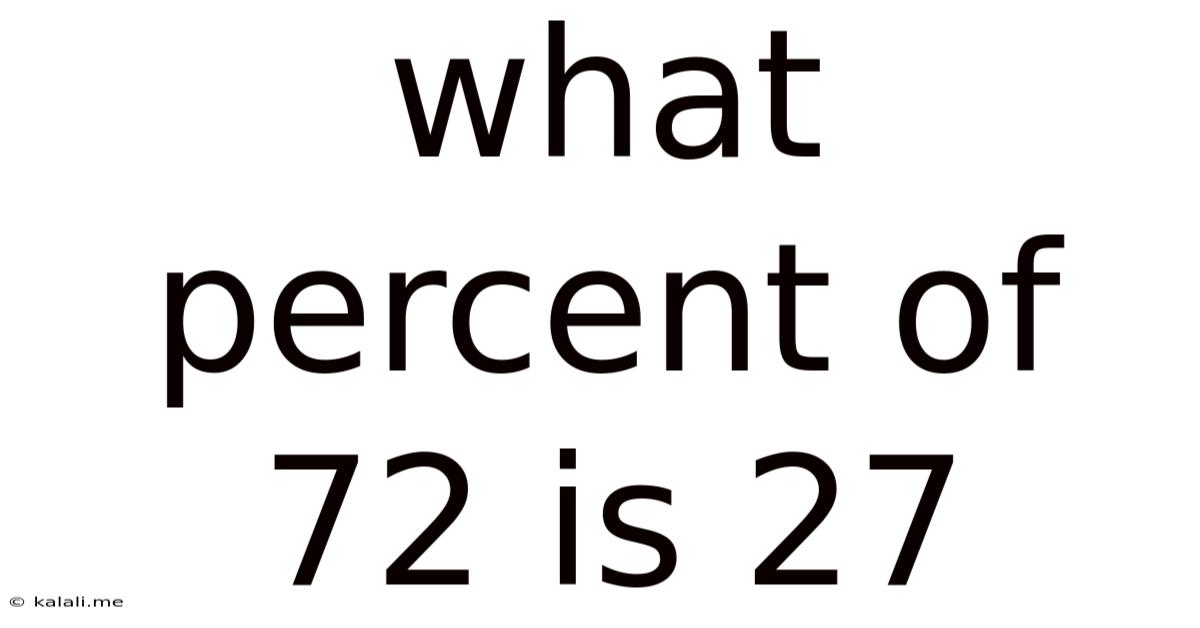
Table of Contents
What Percent of 72 is 27? A Deep Dive into Percentage Calculations
This article will thoroughly explore the question, "What percent of 72 is 27?" We'll not only provide the answer but also delve into the underlying principles of percentage calculations, offering various methods for solving similar problems. Understanding percentages is crucial in various fields, from finance and budgeting to data analysis and scientific research. This guide provides a comprehensive understanding, suitable for students, professionals, and anyone looking to improve their mathematical skills.
Understanding Percentages:
Percentages represent a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5. Percentages are widely used to express proportions, ratios, and changes in values.
Method 1: Using the Proportion Method
This method involves setting up a proportion to solve for the unknown percentage. We can represent the problem as:
- Part/Whole = Percentage/100
In our case:
- Part = 27
- Whole = 72
- Percentage = x (the unknown value we need to find)
Substituting these values into the proportion:
- 27/72 = x/100
To solve for x, we cross-multiply:
- 27 * 100 = 72 * x
- 2700 = 72x
Now, divide both sides by 72:
- x = 2700 / 72
- x = 37.5
Therefore, 27 is 37.5% of 72.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to obtain the percentage.
-
Form a fraction: Express the problem as a fraction: 27/72
-
Simplify the fraction (optional): While not strictly necessary, simplifying the fraction can make the calculation easier. Both 27 and 72 are divisible by 9:
- 27/72 = 3/8
-
Convert to a decimal: Divide the numerator (3) by the denominator (8):
- 3 ÷ 8 = 0.375
-
Convert to a percentage: Multiply the decimal by 100:
- 0.375 * 100 = 37.5%
Therefore, once again, we confirm that 27 is 37.5% of 72.
Method 3: Using the Formula
A more direct formula can be derived from the proportion method:
- Percentage = (Part / Whole) * 100
Substituting our values:
- Percentage = (27 / 72) * 100
- Percentage = 0.375 * 100
- Percentage = 37.5%
This method offers a concise way to calculate percentages directly.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investment. For example, if a store offers a 20% discount on an item originally priced at $100, the discount amount is (20/100) * $100 = $20, and the final price is $80.
-
Data Analysis: Interpreting statistical data, such as survey results, market research, and scientific experiments. For instance, if 60 out of 100 respondents prefer a particular product, the preference rate is (60/100) * 100 = 60%.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, understanding tax rates, and comprehending various proportions. For example, if a recipe calls for 25% of a cup of sugar and the cup holds 8 ounces, you'll need (25/100) * 8 = 2 ounces of sugar.
Beyond the Basics: Solving Inverse Percentage Problems
While the above examples focus on finding the percentage, percentage problems can also involve finding the part or the whole. For instance:
-
Finding the part: What is 37.5% of 72? The answer, as we've already shown, is 27.
-
Finding the whole: 27 is 37.5% of what number? To solve this, we can rearrange the formula:
- Whole = (Part / Percentage) * 100
- Whole = (27 / 37.5) * 100
- Whole = 72
This demonstrates the versatility of percentage calculations and their applicability to various problem-solving scenarios.
Advanced Percentage Concepts:
-
Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase, while a negative result indicates a decrease. Understanding percentage change is crucial when analyzing trends and growth rates.
-
Compound Interest: This refers to interest earned not only on the principal amount but also on the accumulated interest. The formula for compound interest is: A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
-
Percentage Points: This is a crucial distinction, especially when discussing changes in percentages. If a percentage increases from 10% to 15%, it's incorrect to say it increased by 5%; instead, it increased by 5 percentage points (the actual difference).
Conclusion:
The question "What percent of 72 is 27?" is a simple yet powerful illustration of the importance of understanding percentage calculations. We've explored three different methods to solve this problem, demonstrating the flexibility and versatility of percentage concepts. Mastering these calculations is vital for various aspects of life, from personal finance to professional endeavors. By understanding the underlying principles and formulas, one can confidently tackle various percentage-related problems and effectively interpret data presented in percentage form. Remember to always pay attention to the context and choose the most appropriate method for solving the specific problem at hand. The ability to work with percentages accurately and efficiently is a valuable skill that enhances problem-solving abilities and analytical thinking.
Latest Posts
Latest Posts
-
What Is The Lowest Common Multiple Of 10 And 15
Apr 25, 2025
-
Convertidor Metros A Pies Y Pulgadas
Apr 25, 2025
-
How Can I Find The Elevation Of My Home
Apr 25, 2025
-
4 Gallons Equals How Many Liters
Apr 25, 2025
-
How Many Electrons Can The Fourth Energy Level Hold
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 72 Is 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.