What Percent Of 8 Is 3
Kalali
Apr 25, 2025 · 5 min read
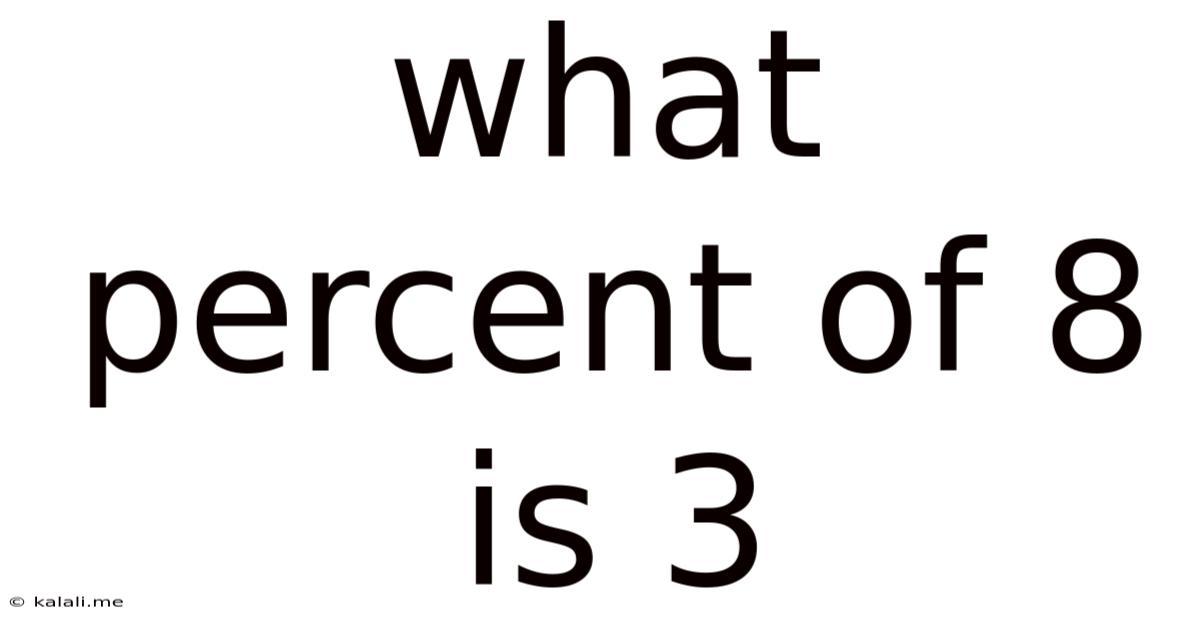
Table of Contents
What Percent of 8 is 3? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 8 is 3?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While a quick calculation can provide the answer, understanding the why behind the calculation is crucial for anyone wanting to master percentages and apply them in various real-world scenarios. This article will not only provide the solution but also delve into the different methods of solving percentage problems, exploring their practical applications and providing a solid foundation for tackling more complex percentage calculations.
Understanding Percentages: A Foundation
Before we dive into solving "What percent of 8 is 3?", let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. This fundamental understanding is key to solving any percentage problem.
Method 1: Using Proportions to Solve Percentage Problems
One of the most effective ways to solve percentage problems is by setting up a proportion. A proportion is an equation stating that two ratios are equal. In the context of our problem, "What percent of 8 is 3?", we can set up the following proportion:
x/100 = 3/8
Here:
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (the whole).
- 3 represents the part.
- 8 represents the whole.
To solve for x, we cross-multiply:
8x = 300
Then, divide both sides by 8:
x = 300/8 = 37.5
Therefore, 3 is 37.5% of 8.
Method 2: Using the Percentage Formula
Another common method involves using the basic percentage formula:
Percentage = (Part / Whole) * 100
In our case:
- Part = 3
- Whole = 8
Substituting these values into the formula:
Percentage = (3 / 8) * 100
Calculating this gives us:
Percentage = 0.375 * 100 = 37.5%
This confirms our previous result: 3 is 37.5% of 8.
Method 3: Understanding the Decimal Equivalent
This method focuses on converting the fraction into a decimal and then expressing it as a percentage. The fraction 3/8 represents the ratio of the part to the whole. Converting 3/8 into a decimal gives us 0.375. To express this decimal as a percentage, we simply multiply it by 100:
0.375 * 100 = 37.5%
This approach reinforces the connection between fractions, decimals, and percentages.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world applications. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. For instance, calculating the interest earned on a savings account or the amount of tax payable on a purchase involves directly applying percentage concepts. Understanding these calculations empowers individuals to make informed financial decisions.
-
Statistics: Percentages are fundamental in presenting and interpreting statistical data. Surveys, polls, and research studies often use percentages to represent proportions and trends. The ability to understand and analyze percentage data is crucial for interpreting research findings and drawing meaningful conclusions.
-
Retail and Sales: Discounts, markups, and sales tax are all expressed as percentages. Retailers use percentages to calculate sale prices, determine profit margins, and understand their pricing strategies. Customers use percentage calculations to determine the actual cost of items after discounts and taxes.
-
Science and Engineering: Percentages are used extensively in various scientific and engineering fields. For example, calculating the efficiency of a machine, determining the concentration of a solution, or analyzing experimental data frequently involves percentage calculations.
-
Everyday Life: From calculating tips at restaurants to understanding the nutritional content of food (percentage of daily value), percentages are integrated into many aspects of daily life. The ability to calculate percentages quickly and accurately is a valuable life skill.
Beyond the Basics: Tackling More Complex Percentage Problems
While "What percent of 8 is 3?" provides a straightforward introduction, many percentage problems are more complex. For instance, you might encounter scenarios where you need to calculate the percentage increase or decrease, find the original value after a percentage change, or work with compound percentages. These scenarios require a deeper understanding of the underlying mathematical principles and the ability to adapt the methods discussed earlier.
Example: Percentage Increase
Let's say a product's price increased from $8 to $10. To calculate the percentage increase, we can use the following formula:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100
In this case:
Percentage Increase = [(10 - 8) / 8] * 100 = 25%
The price increased by 25%.
Example: Finding the Original Value
Suppose a product is on sale for $6 after a 20% discount. To find the original price, we can use the following approach:
The sale price represents 80% (100% - 20%) of the original price. Let x be the original price. Then:
0.8x = 6
Solving for x:
x = 6 / 0.8 = $7.50
The original price was $7.50.
Mastering Percentages: A Continuous Learning Process
The ability to calculate percentages accurately and efficiently is a valuable skill applicable across various domains. While solving "What percent of 8 is 3?" might seem simple, it serves as a gateway to understanding the broader world of percentage calculations. By mastering the fundamental principles and practicing different methods, you can confidently tackle more complex percentage problems and apply this essential skill in your personal and professional life. Remember that consistent practice and a deeper understanding of the underlying mathematical concepts are key to mastering this crucial aspect of mathematics. The more you practice, the more intuitive and efficient your calculations will become. This will not only improve your problem-solving skills but also enhance your overall numeracy.
Latest Posts
Latest Posts
-
Least Common Multiple Of 9 And 5
Apr 25, 2025
-
What Pattern Do You Notive When Square Numbers
Apr 25, 2025
-
How Many Lines Of Symmetry Does Circle Have
Apr 25, 2025
-
63 Inches In Feet In Cm
Apr 25, 2025
-
El Huracan Mas Fuerte De La Historia
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 8 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.