What Percent Of 9 Is 1
Kalali
Apr 25, 2025 · 5 min read
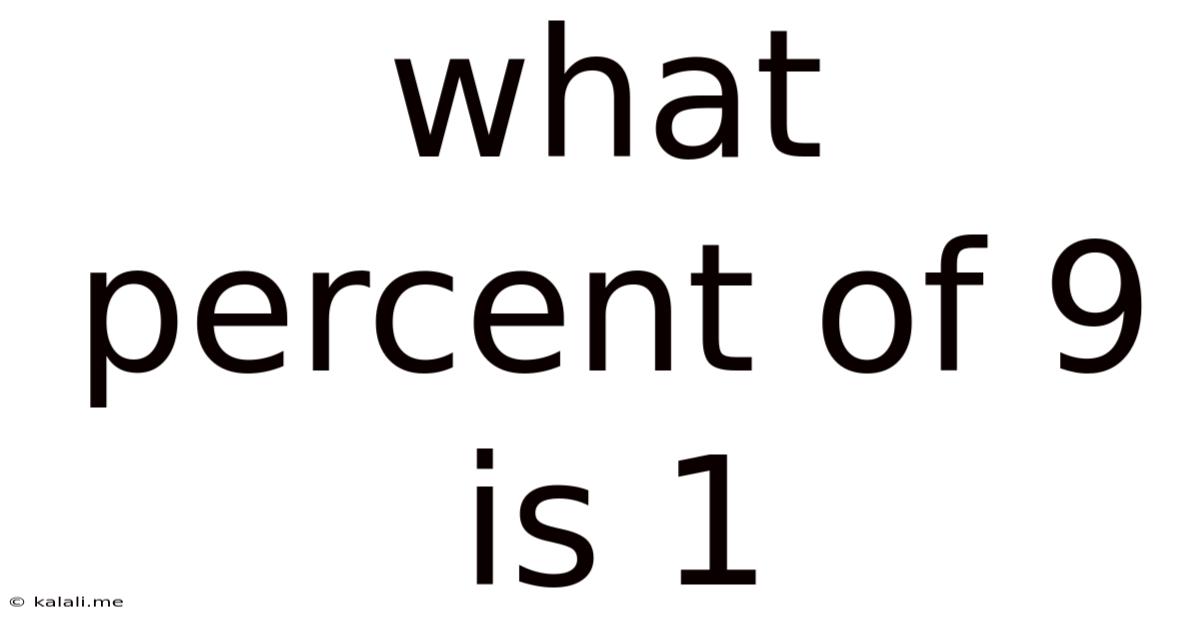
Table of Contents
What Percent of 9 is 1? Unpacking the Basics of Percentages and Problem Solving
This seemingly simple question – "What percent of 9 is 1?" – actually opens the door to understanding a fundamental mathematical concept: percentages. While the answer might seem immediately obvious to some, delving deeper reveals the underlying principles and provides a solid foundation for tackling more complex percentage problems. This article will not only answer the question but also explore the various methods of solving it, explain the core concepts behind percentages, and provide practical examples to solidify your understanding. This comprehensive guide will equip you with the skills to confidently tackle any percentage calculation.
Meta Description: Learn how to calculate percentages with a step-by-step guide explaining how to determine what percent of 9 is 1. Master the basics and advanced techniques for solving percentage problems.
Understanding Percentages: The Building Blocks
Before we dive into the specific problem, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This fundamental understanding is crucial for tackling all percentage-related problems.
Understanding percentages involves three key components:
- The Part: This represents the smaller portion of the whole. In our problem, "1" is the part.
- The Whole: This is the total amount or the entire quantity being considered. In our case, "9" is the whole.
- The Percentage: This is the proportion of the part relative to the whole, expressed as a number out of 100. This is what we need to find.
Method 1: Using the Formula
The most straightforward method to determine what percent of 9 is 1 involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
Let's plug in the values from our problem:
(1 / 9) * 100% = Percentage
Calculating this gives us:
0.1111... * 100% ≈ 11.11%
Therefore, 1 is approximately 11.11% of 9. The "..." indicates that the decimal 0.1111... is a repeating decimal, extending infinitely. For practical purposes, we round the percentage to two decimal places.
Method 2: Proportion Method
Another effective approach is using proportions. We can set up a proportion to solve for the unknown percentage (let's represent it as 'x'):
1/9 = x/100
To solve for 'x', we cross-multiply:
9x = 100
x = 100/9
x ≈ 11.11
Therefore, x, representing the percentage, is approximately 11.11%. This method reinforces the concept of percentages as a comparison of two quantities.
Method 3: Using Decimal Conversion
We can also solve this by converting the fraction to a decimal and then converting the decimal to a percentage.
1/9 ≈ 0.1111...
To convert this decimal to a percentage, we simply multiply by 100%:
0.1111... * 100% ≈ 11.11%
This method highlights the direct relationship between fractions, decimals, and percentages.
Addressing the Repeating Decimal: Precision and Practical Application
It's important to acknowledge the repeating decimal (0.1111...) that arises in this calculation. This emphasizes that not all percentage calculations result in neat, whole numbers. The level of precision required depends on the context. For everyday purposes, rounding to two decimal places (11.11%) is usually sufficient. However, in scientific or engineering applications, greater accuracy might be necessary. Understanding how to handle these repeating decimals is crucial for accurate calculations.
Expanding on Percentage Applications: Real-World Examples
Understanding percentages extends far beyond simple mathematical exercises. They are integral to various aspects of daily life, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase requires a strong grasp of percentages.
-
Statistics: Percentages are used extensively in statistics to represent data, proportions, and probabilities. For example, analyzing survey results, understanding demographic distributions, and interpreting scientific studies all involve working with percentages.
-
Science: Percentages are essential in many scientific disciplines, such as chemistry (concentration of solutions), biology (population growth rates), and physics (efficiency of machines).
-
Everyday Life: Calculating tips at restaurants, figuring out sale prices, or understanding nutritional information on food labels involves percentages.
Advanced Percentage Problems: Building Your Skills
While the initial problem was relatively straightforward, mastering percentage calculations requires the ability to tackle more complex scenarios. Here are some examples of more advanced percentage problems:
-
Finding the Whole: If 25% of a number is 10, what is the number?
-
Finding the Part: What is 30% of 150?
-
Percentage Increase/Decrease: A product's price increased by 15% from $50. What is the new price?
-
Compound Interest: Calculate the final amount after 3 years with a principal of $1000, an interest rate of 5% compounded annually.
Solving these more advanced problems involves applying the same fundamental principles but often requires multiple steps and a deeper understanding of the underlying concepts.
Conclusion: Mastering Percentages for Success
This in-depth exploration of the seemingly simple question, "What percent of 9 is 1?", has revealed the multifaceted nature of percentage calculations. From the basic formula to the various solution methods, we have demonstrated the importance of understanding the core concepts of the part, the whole, and the percentage itself. The examples provided highlight the extensive applications of percentages in various fields, reinforcing the practical relevance of this fundamental mathematical skill. By grasping these principles and practicing with different types of problems, you can confidently navigate the world of percentages and apply this crucial skill to numerous real-world situations. Remember to practice regularly, explore different problem-solving approaches, and don’t be afraid to tackle challenging problems to solidify your understanding. The more you practice, the more comfortable and proficient you'll become in tackling any percentage-related challenge.
Latest Posts
Latest Posts
-
Write The Chemical Equation For Cellular Respiration
Apr 28, 2025
-
What Is 40 Degrees C In F
Apr 28, 2025
-
2 Is What Percent Of 100
Apr 28, 2025
-
What Percentage Is 39 Out Of 50
Apr 28, 2025
-
160 Cm En Pies Y Pulgadas
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 9 Is 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.