What Percent Of 90 Is 25
Kalali
Apr 25, 2025 · 5 min read
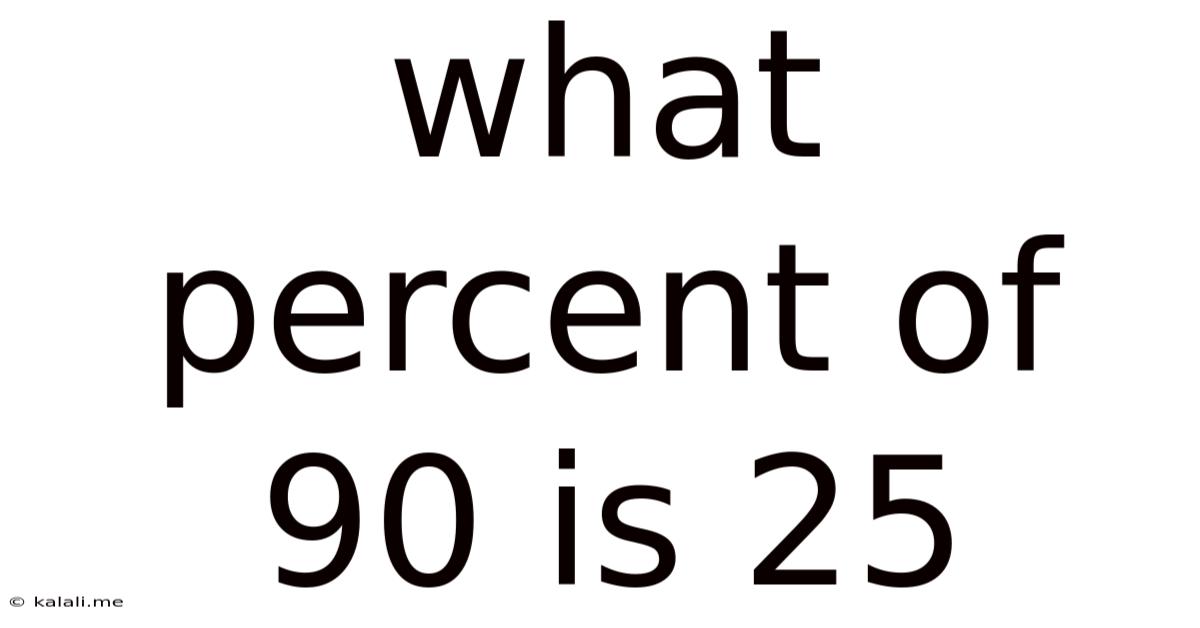
Table of Contents
What Percent of 90 is 25? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 90 is 25?", opens the door to a broader understanding of percentage calculations, their applications in various fields, and even the underlying mathematical principles. While the answer itself is straightforward, the journey to understanding how to arrive at that answer, and how to apply this knowledge to more complex scenarios, is far more enriching. This article will not only provide the solution but will also explore the various methods for calculating percentages, delve into practical examples, and discuss the importance of percentage calculations in everyday life and professional settings.
Meta Description: Learn how to calculate percentages with a detailed explanation of finding what percent of 90 is 25. This guide covers multiple methods, real-world applications, and advanced percentage problems.
To begin, let's answer the core question: What percent of 90 is 25?
The most direct way to solve this is through a simple equation:
- x/100 * 90 = 25
Where 'x' represents the percentage we're trying to find. Solving for 'x':
- Multiply both sides by 100: 90x = 2500
- Divide both sides by 90: x = 2500/90
- Simplify the fraction: x ≈ 27.78
Therefore, 25 is approximately 27.78% of 90.
Different Approaches to Percentage Calculations
While the above method is efficient, understanding different approaches provides a more robust grasp of percentage calculations. Let's explore a few alternatives:
1. Using Proportions:
Percentage problems can be effectively solved using proportions. We can set up a proportion as follows:
- 25/90 = x/100
This states that the ratio of 25 to 90 is equal to the ratio of x (our unknown percentage) to 100. Cross-multiplying and solving for x gives us the same result as before: x ≈ 27.78.
2. Using Decimal Conversion:
This method involves converting the percentage to a decimal. We can express the problem as:
- x * 0.90 = 25
Where 0.90 is the decimal equivalent of 90%. Solving for x:
- x = 25 / 0.90
- x ≈ 27.78
3. Using the Percentage Formula:
The fundamental percentage formula is:
- (Part / Whole) * 100 = Percentage
In our case:
- (25 / 90) * 100 ≈ 27.78%
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for managing personal finances and making informed investment decisions. For instance, understanding a 5% interest rate on a loan or a 20% discount on a purchase requires accurate percentage calculations.
-
Retail and Sales: Businesses use percentages to determine discounts, markups, and sales tax. Calculating profit margins and understanding sales performance also involves percentage analysis. A store offering a 30% off sale needs to accurately calculate the discounted price to ensure correct billing and avoid losses.
-
Science and Statistics: Percentages are frequently used in scientific research to represent data proportions, probability, and statistical significance. For example, reporting the percentage of participants in a study who responded positively to a treatment requires accurate percentage calculations. Understanding statistical significance and confidence intervals heavily involves percentages.
-
Education: Grade calculation, test scores, and performance evaluation often involve percentages. A student's final grade might be calculated as a weighted average of multiple assessments, each expressed as a percentage.
-
Everyday Life: Calculating tips at restaurants, determining the percentage of ingredients in a recipe, or understanding nutritional information on food labels all use percentage calculations. Understanding percentages helps us make informed decisions in our daily lives.
Advanced Percentage Problems and Applications
The fundamental understanding of percentages allows us to tackle more complex problems:
1. Finding the Whole when the Percentage and Part are Known:
Suppose you know that 30% of a number is 60. To find the whole number, you would set up the equation:
- 0.30 * x = 60
Solving for x:
- x = 60 / 0.30 = 200
2. Finding the Percentage Increase or Decrease:
Calculating percentage changes is essential in tracking growth or decline. The formula is:
- [(New Value - Old Value) / Old Value] * 100 = Percentage Change
A positive result indicates an increase, while a negative result signifies a decrease.
3. Compound Interest Calculations:
Compound interest involves earning interest on both the principal amount and accumulated interest. The formula for compound interest is:
- A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is crucial for long-term financial planning.
4. Percentage Points vs. Percentages:
It's important to distinguish between percentage points and percentages. A change of 10 percentage points means a direct difference of 10%, while a 10% increase on a base percentage requires a calculation. For example, increasing from 20% to 30% is a 10 percentage point increase but a 50% increase in the percentage itself.
Conclusion: Mastering Percentage Calculations for Success
Understanding percentages is not just about solving simple equations; it's about developing a skill that's crucial for success in various fields. From personal finance to scientific research, the ability to perform accurate percentage calculations and understand their implications is invaluable. By mastering the different methods and applying them to real-world problems, you can confidently navigate situations involving percentages and make better-informed decisions. The simple question of "What percent of 90 is 25?" serves as a springboard to a deeper understanding of this fundamental mathematical concept and its widespread applications. The more you practice and apply these methods, the more intuitive and efficient your percentage calculations will become. Remember to always double-check your work, especially in situations where accuracy is critical, such as financial calculations or scientific data analysis. Using a calculator can help ensure accuracy, but it's equally important to understand the underlying principles and be able to perform the calculations manually.
Latest Posts
Latest Posts
-
How Can I Find The Elevation Of My Home
Apr 25, 2025
-
4 Gallons Equals How Many Liters
Apr 25, 2025
-
How Many Electrons Can The Fourth Energy Level Hold
Apr 25, 2025
-
Glass Breaking Is A Physical Change
Apr 25, 2025
-
What Is The Square Root Of 162
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 90 Is 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.