What Percentage Is 15 Of 20
Kalali
Mar 08, 2025 · 5 min read
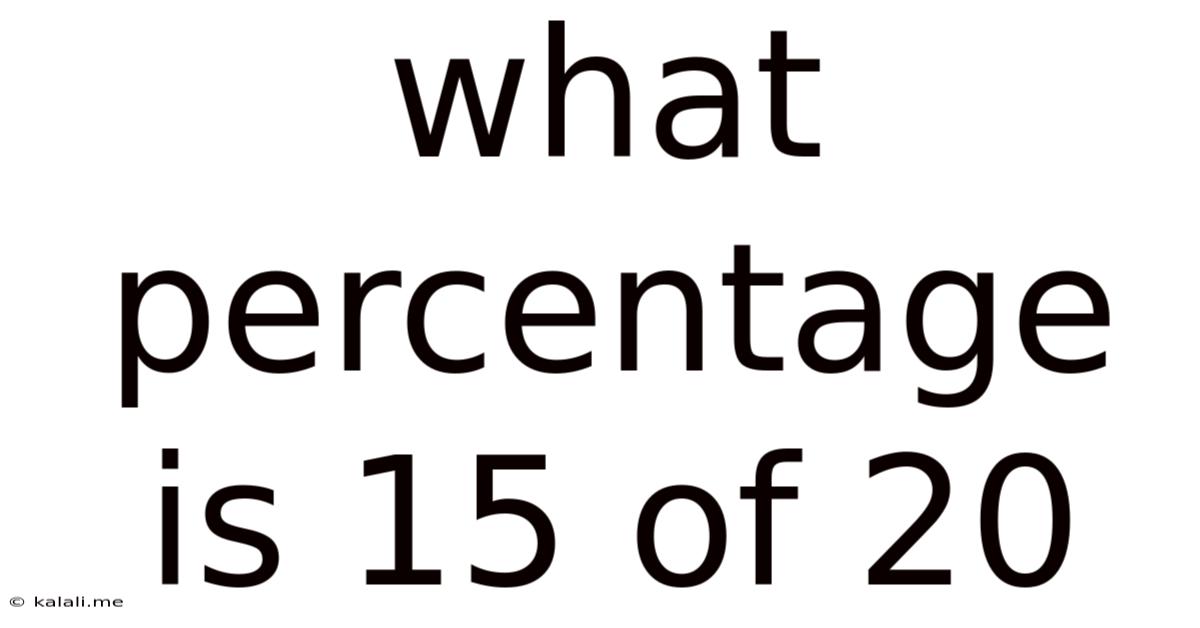
Table of Contents
What Percentage is 15 of 20? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for informed decision-making and accurate interpretations of data. This article will delve into the simple yet powerful method of calculating percentages, using the example of "What percentage is 15 of 20?" as a springboard to explore broader concepts and applications.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (Latin: per centum). Therefore, 15% means 15 out of 100, or 15/100. This fraction can be simplified to 3/20. Understanding this fundamental definition is key to solving percentage problems.
Calculating "What Percentage is 15 of 20?"
To find what percentage 15 represents of 20, we follow a simple three-step process:
Step 1: Set up the Fraction:
Represent the problem as a fraction: 15/20. This fraction signifies that 15 is a part of the whole, which is 20.
Step 2: Convert the Fraction to a Decimal:
Divide the numerator (15) by the denominator (20): 15 ÷ 20 = 0.75
Step 3: Convert the Decimal to a Percentage:
Multiply the decimal by 100 and add the percent symbol (%): 0.75 x 100 = 75%.
Therefore, 15 is 75% of 20.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are other approaches that can be equally effective, particularly when dealing with more complex calculations or when using calculators or spreadsheets:
Method 1: Using a Proportion:
A proportion sets two ratios equal to each other. We can set up a proportion to solve for the unknown percentage (x):
15/20 = x/100
To solve for x, cross-multiply:
20x = 1500
x = 1500/20
x = 75
Therefore, x = 75%, confirming our previous result. This method is especially helpful when visualizing the relationship between the parts and the whole.
Method 2: Using a Calculator:
Most calculators have a percentage function. Simply input 15 ÷ 20 and then multiply the result by 100. The calculator will directly provide the answer: 75%. This method is quick and efficient, especially for repetitive calculations.
Method 3: Using Spreadsheets:
Spreadsheets like Microsoft Excel or Google Sheets have built-in functions for percentage calculations. The formula =15/20 will give you the decimal equivalent (0.75), and formatting the cell as a percentage will automatically convert it to 75%. This approach is ideal for handling large datasets and automating percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple arithmetic exercises. Its applications span numerous fields, including:
Finance and Budgeting:
- Calculating interest: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations allows for accurate calculation of interest earned or paid.
- Analyzing financial statements: Financial statements like income statements and balance sheets use percentages extensively to express ratios and trends. Analyzing these percentages is crucial for evaluating financial performance.
- Tax calculations: Income taxes, sales taxes, and other taxes are often calculated as percentages of income or the value of goods and services.
- Discount calculations: Sales and discounts are usually expressed as percentages, requiring percentage calculations to determine the final price.
Science and Statistics:
- Data analysis: Percentages are frequently used to represent data in various forms, including charts, graphs, and tables. Understanding percentage calculations is crucial for interpreting and analyzing statistical data.
- Probability and statistics: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
- Scientific measurements: Certain scientific measurements, particularly in chemistry and physics, utilize percentages to express concentrations or proportions.
Business and Marketing:
- Market share analysis: Market share is often expressed as a percentage, indicating the proportion of the market held by a particular company or product.
- Sales performance tracking: Tracking sales performance often involves comparing sales figures to targets, expressed as percentages.
- Customer satisfaction surveys: Customer satisfaction is frequently measured using percentages to represent the level of satisfaction among customers.
- Conversion rate optimization: Analyzing conversion rates, such as the percentage of website visitors who make a purchase, is crucial for optimizing marketing strategies.
Everyday Life:
- Shopping and budgeting: Calculating discounts, sales tax, and tips often involves percentage calculations.
- Recipe adjustments: Scaling recipes up or down requires understanding percentage calculations to maintain the correct proportions of ingredients.
- Understanding statistics in news and media: Many news reports and articles use percentages to present data, requiring an understanding of percentage calculations for informed interpretation.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, certain common mistakes should be avoided:
- Incorrect order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when calculating percentages involving multiple steps.
- Confusing percentages with decimals: Remember to convert decimals to percentages by multiplying by 100 and vice-versa by dividing by 100.
- Rounding errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Round only at the final step if possible to maintain accuracy.
- Incorrect interpretation of percentages: Pay attention to the context of the problem to ensure you are interpreting the percentage correctly. For instance, a 20% increase is different from a 20% decrease.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with far-reaching applications in various aspects of daily life, academic pursuits, and professional careers. By understanding the fundamental concepts and employing the various calculation methods discussed, you can confidently tackle percentage problems, analyze data effectively, and make informed decisions based on accurate numerical interpretations. Remember to practice regularly and always double-check your work to ensure accuracy. The ability to effortlessly compute percentages will serve as a significant asset in your personal and professional endeavors.
Latest Posts
Latest Posts
-
How Many Cups Of Milk Are In A Half Gallon
Jun 30, 2025
-
How Many Ritz Crackers In A Cup
Jun 30, 2025
-
How Many 16 9 Oz Bottles Make A Half Gallon
Jun 30, 2025
-
How Many Times Does 3 Go Into 24
Jun 30, 2025
-
What Year Was I Born If Im 15
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 15 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.