What Percentage Is 15 Out Of 50
Kalali
Apr 25, 2025 · 5 min read
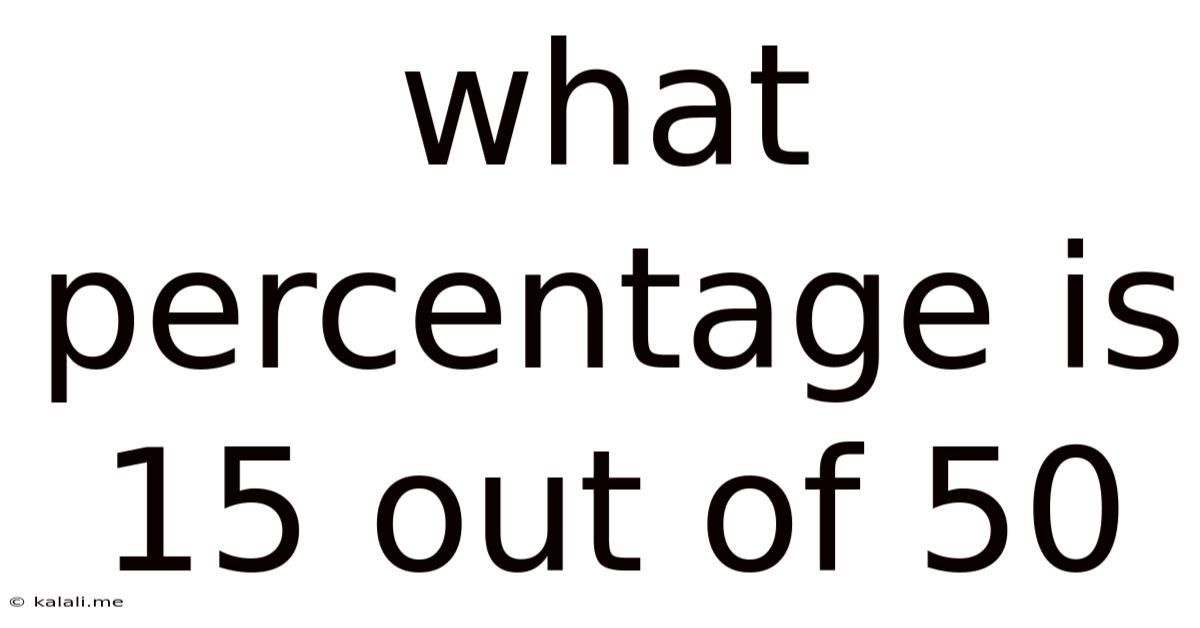
Table of Contents
What Percentage is 15 out of 50? A Deep Dive into Percentage Calculations and Real-World Applications
Meta Description: Uncover the simple calculation of 15 out of 50 as a percentage, explore different methods for solving similar problems, and discover real-world applications of percentage calculations across various fields. Learn how to confidently tackle percentage problems and improve your math skills.
Calculating percentages is a fundamental skill applicable across numerous aspects of life, from academic pursuits to professional fields. Understanding how to determine percentages allows you to interpret data effectively, make informed decisions, and solve problems accurately. This article will meticulously explore the question, "What percentage is 15 out of 50?", providing a detailed explanation of the calculation and delving into various methods to arrive at the answer. We'll also investigate the practical uses of percentage calculations in everyday scenarios.
The Simple Calculation: 15 out of 50 as a Percentage
The most straightforward method to determine what percentage 15 represents out of 50 involves converting the fraction 15/50 into a percentage. Remember, a percentage is simply a fraction expressed out of 100.
Step 1: Express the values as a fraction.
The problem "What percentage is 15 out of 50?" can be written as the fraction 15/50.
Step 2: Convert the fraction to a decimal.
To convert the fraction 15/50 to a decimal, we divide the numerator (15) by the denominator (50):
15 ÷ 50 = 0.3
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.3 x 100 = 30%
Therefore, 15 out of 50 is 30%.
Alternative Methods for Calculating Percentages
While the above method is the most direct approach, alternative methods can enhance understanding and provide flexibility in solving percentage problems. Let's explore a few:
Method 1: Using Proportions
This method utilizes the concept of proportional relationships. We can set up a proportion to solve for the unknown percentage (x):
15/50 = x/100
To solve for x, we cross-multiply:
50x = 1500
Then, divide both sides by 50:
x = 1500/50 = 30
Therefore, x = 30%, confirming our previous result.
Method 2: Simplifying the Fraction
Simplifying the fraction before converting to a decimal can sometimes make the calculation easier. The fraction 15/50 can be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 5:
15 ÷ 5 = 3 50 ÷ 5 = 10
This simplifies the fraction to 3/10. Now, converting this simplified fraction to a decimal is easier:
3 ÷ 10 = 0.3
Converting 0.3 to a percentage yields 30%, as before.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and loan repayments all rely heavily on percentage calculations. For example, understanding the interest rate on a loan or credit card is crucial for managing finances effectively. Similarly, calculating sales tax or discounts at the store requires accurate percentage computation.
-
Academics: Grading systems, test scores, and statistical analysis in research often utilize percentages. A student's grade point average (GPA) is often expressed as a percentage. Researchers frequently present their findings using percentages to illustrate trends and relationships within their data sets.
-
Retail: Businesses use percentages extensively for pricing, sales, discounts, and profit calculations. Understanding markups and margins is essential for maintaining profitability. Sales and promotions are often advertised as percentage discounts to attract customers.
-
Science and Engineering: Percentage calculations are critical in fields like chemistry (concentration of solutions), physics (efficiency of machines), and engineering (design parameters). Determining the concentration of a chemical solution or calculating the efficiency of a machine involves precise percentage calculations.
-
Sports Statistics: Numerous sports statistics use percentages to express performance metrics. Batting averages in baseball, free throw percentages in basketball, and completion percentages in American football all rely on percentage calculations.
Advanced Percentage Calculations: Beyond the Basics
While the calculation of 15 out of 50 is relatively simple, understanding more complex percentage problems is beneficial. Let's examine some scenarios:
-
Calculating a percentage increase or decrease: This involves determining the percentage change between two values. For instance, if a price increases from $50 to $60, the percentage increase is calculated as follows:
(Increase/Original Value) x 100% = ((60-50)/50) x 100% = 20%
-
Finding the original value after a percentage change: If a price is reduced by 20% to $40, the original price can be calculated by working backward. Let x be the original price. Then:
x - 0.20x = $40 0.80x = $40 x = $40 / 0.80 = $50
-
Percentage of a percentage: Sometimes, you'll need to calculate a percentage of a percentage. For example, finding 10% of 20% of 100:
0.10 x (0.20 x 100) = 2
These examples highlight the versatility and importance of percentage calculations across various numerical applications.
Mastering Percentage Calculations: Tips and Resources
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying principles. Here are some tips to improve your proficiency:
-
Practice regularly: Work through various percentage problems to reinforce your understanding and build confidence.
-
Use different methods: Experiment with different approaches (fractions, decimals, proportions) to find the method that best suits your understanding.
-
Visual aids: Diagrams or charts can sometimes be helpful in visualizing percentage problems, particularly when dealing with complex scenarios.
-
Online resources: Numerous online resources, including educational websites and calculators, can provide additional practice problems and explanations.
-
Seek help when needed: Don't hesitate to ask for clarification or assistance if you encounter difficulties.
Conclusion: The Importance of Percentage Understanding
Understanding how to calculate percentages is a critical skill with wide-ranging applications in various fields. This article has demonstrated the simple calculation of "What percentage is 15 out of 50?", explained alternative methods, and explored real-world applications. By mastering these techniques and practicing regularly, you can improve your numerical abilities and confidently tackle percentage problems in any context. The ability to accurately calculate and interpret percentages empowers you to make informed decisions, analyze data effectively, and succeed in various aspects of life, both personal and professional. Remember to practice, explore different methods, and utilize resources to enhance your understanding. The ability to confidently handle percentage calculations is a valuable asset that will serve you well throughout your life.
Latest Posts
Latest Posts
-
8 Cups Of Water In Ml
Apr 28, 2025
-
4 1 4 As An Improper Fraction
Apr 28, 2025
-
Cuales Son Los Centimetros En Un Metro
Apr 28, 2025
-
How Much Is 170 Cm In Inches
Apr 28, 2025
-
What Was Darwin Influences On Lyell And Hutton
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 15 Out Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.