What Percentage Is 18 Of 24
Kalali
Apr 19, 2025 · 5 min read
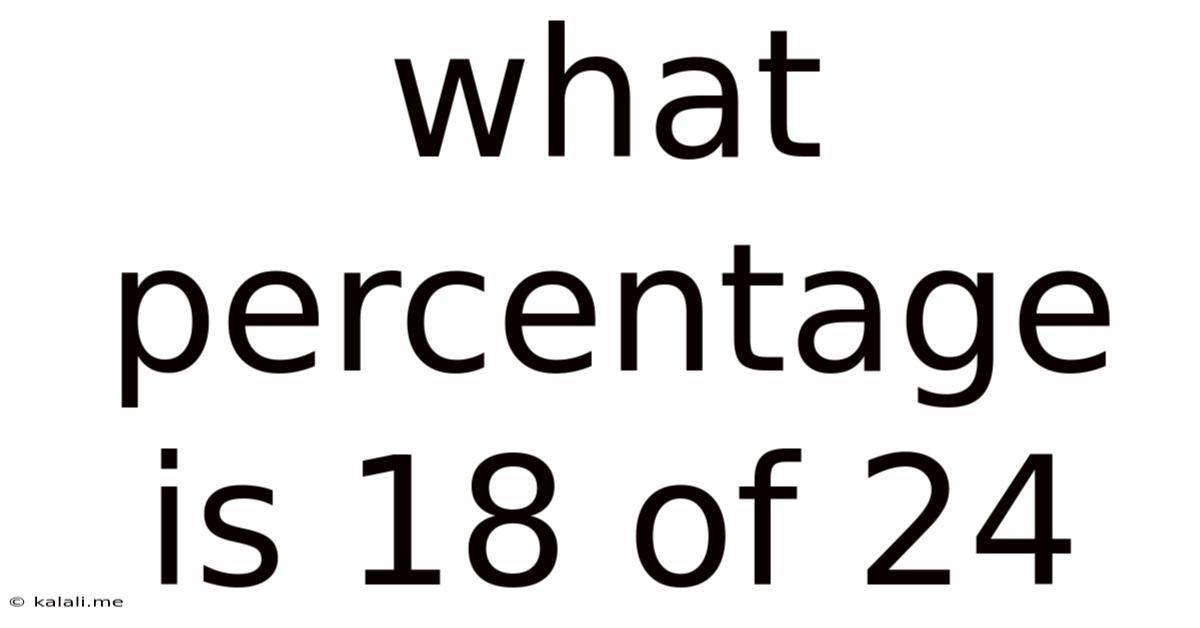
Table of Contents
What Percentage is 18 of 24? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This seemingly simple question – "What percentage is 18 of 24?" – opens the door to a deeper understanding of percentage calculations, their applications, and how to approach similar problems with confidence. This article will not only answer the question directly but also explore the underlying principles, provide alternative methods for calculation, and demonstrate the broader context of percentages in everyday life.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide answers "What percentage is 18 of 24?" and explains various methods for solving percentage problems, including practical applications and real-world examples.
The Direct Calculation: Finding the Percentage
The most straightforward way to determine what percentage 18 represents of 24 is through a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 18
- Whole: 24
Therefore, the calculation is:
(18 / 24) * 100% = 75%
Therefore, 18 is 75% of 24.
This fundamental formula provides the bedrock for understanding percentage calculations. It’s applicable across various scenarios, requiring only the identification of the "part" and the "whole."
Alternative Methods: Exploring Different Approaches
While the above method is the most direct, several alternative approaches can help solidify understanding and provide flexibility in problem-solving:
Method 1: Using Fractions
Percentages can be expressed as fractions. The fraction 18/24 simplifies to 3/4. To convert this fraction to a percentage, we simply divide the numerator by the denominator and multiply by 100%:
(3 / 4) * 100% = 75%
This method highlights the inherent relationship between fractions and percentages, offering an alternative perspective on the calculation. Simplifying fractions before converting to percentages often streamlines the process.
Method 2: Proportion Method
The proportion method employs the concept of ratios to solve percentage problems. We can set up a proportion:
18/24 = x/100
Where 'x' represents the percentage we are trying to find. Solving for 'x' involves cross-multiplication:
24x = 1800
x = 1800 / 24
x = 75
This method demonstrates the power of proportionality in solving percentage-related problems and provides a structured approach, particularly useful for more complex scenarios.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. The fraction 18/24, simplified to 3/4, is equivalent to the decimal 0.75. To convert this decimal to a percentage, simply multiply by 100%:
0.75 * 100% = 75%
This method emphasizes the interconnectedness of fractions, decimals, and percentages, offering a versatile approach to percentage calculations.
Understanding the Context: Real-World Applications
The ability to calculate percentages extends far beyond simple mathematical exercises. It's an essential skill applied across numerous fields:
Finance and Budgeting:
- Calculating interest rates: Understanding interest on loans, savings accounts, and investments relies heavily on percentage calculations.
- Analyzing financial statements: Profit margins, expense ratios, and return on investment (ROI) all involve percentage calculations.
- Managing personal finances: Budgeting, tracking expenses, and saving effectively require a grasp of percentages.
Sales and Marketing:
- Calculating discounts and markups: Determining sale prices, profit margins, and the impact of discounts all use percentage calculations.
- Analyzing sales data: Tracking sales growth, market share, and conversion rates relies heavily on percentage calculations.
- Understanding market research: Interpreting survey data and analyzing consumer behavior often requires the interpretation of percentages.
Education and Science:
- Calculating grades and scores: Converting raw scores to percentages and calculating final grades frequently involves percentage calculations.
- Analyzing statistical data: Expressing data as percentages helps in comparison and interpretation of results in scientific research.
- Understanding probability: Percentages are crucial in expressing and interpreting probabilities in various fields.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants requires percentage calculations.
- Understanding tax rates: Calculating sales tax, income tax, and other taxes involves percentage calculations.
- Comparing prices: Determining which product offers better value based on price and quantity often involves percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While the "18 is what percent of 24" problem provides a foundational understanding, many real-world scenarios present more complex challenges. These often involve:
- Finding the whole when the part and percentage are known: For example, "If 30% of a number is 60, what is the number?"
- Finding the part when the whole and percentage are known: For example, "What is 25% of 80?"
- Calculating percentage change: Determining the percentage increase or decrease between two values, such as calculating the percentage growth in sales over time.
- Compound percentages: Calculating percentages upon percentages, such as compound interest calculations.
Mastering the basic formula and understanding the underlying principles allows for tackling these more complex scenarios with confidence. Practice is key to developing proficiency in solving various percentage problems.
Using Technology for Percentage Calculations
Many readily available tools can assist in performing percentage calculations, particularly for more complex scenarios:
- Spreadsheets (Excel, Google Sheets): Spreadsheets offer built-in functions for percentage calculations, simplifying complex computations and allowing for data analysis.
- Calculators: Most calculators include a percentage function, streamlining the calculation process.
- Online Percentage Calculators: Numerous online calculators are available, providing a convenient way to perform percentage calculations quickly and easily.
These tools can be invaluable in solving percentage problems efficiently, particularly in situations involving large datasets or complex calculations.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a crucial skill with widespread applications in various aspects of life. The seemingly simple question, "What percentage is 18 of 24?" serves as a gateway to mastering this fundamental concept. By understanding the basic formula, exploring alternative methods, and recognizing the broader applications of percentage calculations, one can confidently approach various quantitative challenges and make informed decisions in diverse situations. Remember that practice and the utilization of available tools further enhance proficiency and efficiency in solving percentage-related problems. This comprehensive understanding of percentages empowers individuals to navigate the complexities of numerical analysis and make informed decisions in both professional and personal contexts.
Latest Posts
Latest Posts
-
What Is 30 100 As A Percent
Apr 22, 2025
-
How To Find The Range In A Dot Plot
Apr 22, 2025
-
As Altitude Increases What Happens To Air Pressure
Apr 22, 2025
-
How Big Is 36 Inches In Cm
Apr 22, 2025
-
What Is 0 125 In A Fraction
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 18 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.