What Percentage Is 2 Of 6
Kalali
Apr 16, 2025 · 5 min read
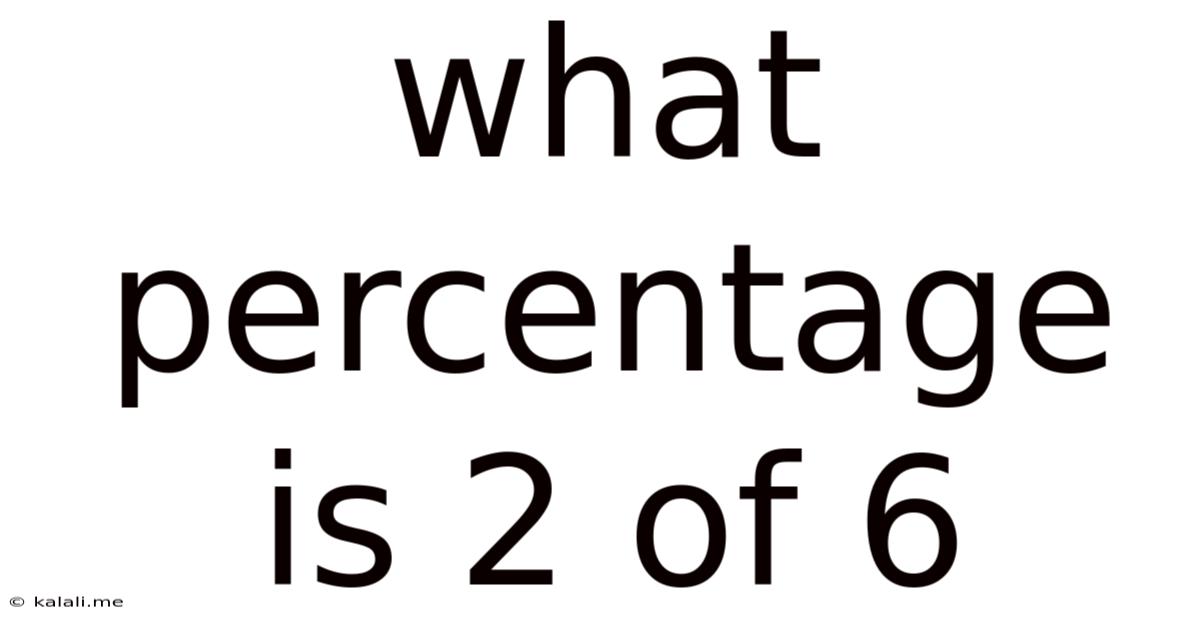
Table of Contents
What Percentage is 2 of 6? A Deep Dive into Percentage Calculations and Their Applications
Meta Description: Understanding percentages is crucial in various aspects of life. This comprehensive guide explains how to calculate what percentage 2 is of 6, explores different methods, and demonstrates practical applications across diverse fields. Learn about percentage increase, decrease, and error calculations, plus how to solve percentage problems efficiently.
Calculating percentages is a fundamental skill with broad applications in everyday life, from understanding sales discounts and interest rates to analyzing data and interpreting statistical information. This article will thoroughly explore the question, "What percentage is 2 of 6?", providing a step-by-step guide to calculating this and other similar percentages, as well as delving into the broader context of percentage calculations and their real-world applications.
Understanding the Basics of Percentages
Before we delve into calculating what percentage 2 is of 6, let's establish a solid foundation in percentage basics. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
The key to understanding percentages lies in recognizing the relationship between the part, the whole, and the percentage. The formula we use is:
(Part / Whole) * 100 = Percentage
In our example, "What percentage is 2 of 6?", 2 is the part and 6 is the whole.
Calculating "What Percentage is 2 of 6?"
Now, let's apply the formula to answer our question:
(2 / 6) * 100 = Percentage
-
Divide the part by the whole: 2 divided by 6 equals 0.3333... (a recurring decimal).
-
Multiply by 100: 0.3333... multiplied by 100 equals 33.33...
Therefore, 2 is approximately 33.33% of 6. The recurring decimal indicates that this is an infinitely repeating decimal, so we typically round it to a certain number of decimal places depending on the required level of precision. In many contexts, rounding to two decimal places (33.33%) is sufficient.
Alternative Methods for Calculating Percentages
While the formula above is the most straightforward, there are alternative approaches depending on your preference and the complexity of the problem.
-
Using Proportions: You can set up a proportion to solve for the percentage:
2/6 = x/100
Cross-multiplying gives: 6x = 200
Solving for x: x = 200/6 = 33.33...
-
Using Decimal Conversion: First, convert the fraction 2/6 to a decimal by dividing 2 by 6 (0.3333...). Then, multiply the decimal by 100 to express it as a percentage (0.3333... * 100 = 33.33%).
Practical Applications of Percentage Calculations
Percentage calculations are vital in various aspects of daily life and professional settings. Here are some examples:
-
Sales and Discounts: Stores often advertise discounts as percentages (e.g., "20% off"). Understanding percentages helps consumers calculate the final price after a discount.
-
Finance and Investments: Interest rates on loans, savings accounts, and investments are typically expressed as percentages. Calculating these percentages is essential for financial planning and understanding investment returns.
-
Taxes: Taxes are often calculated as a percentage of income or the value of goods and services. Knowing how to calculate tax percentages helps individuals and businesses understand their financial obligations.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions and trends within data sets. This is crucial for interpreting research findings, market analysis, and other data-driven decision-making.
-
Science and Engineering: Percentages are employed in various scientific and engineering calculations, such as calculating efficiency, error rates, and concentration levels.
-
Everyday Life: From calculating tips in restaurants to understanding survey results, percentages are ubiquitous in our daily interactions.
Percentage Increase and Decrease
Beyond calculating a simple percentage of a whole, understanding percentage increase and decrease is equally important.
-
Percentage Increase: This calculates the percentage change when a value increases. The formula is:
[(New Value - Original Value) / Original Value] * 100For example, if a product's price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] * 100 = 20% -
Percentage Decrease: This calculates the percentage change when a value decreases. The formula is:
[(Original Value - New Value) / Original Value] * 100If the same product's price decreases from $12 to $9, the percentage decrease is:
[(12 - 9) / 12] * 100 = 25%
Percentage Error Calculation
Percentage error is a measure of the accuracy of a measurement or calculation compared to the true or accepted value. The formula is:
[|Measured Value - True Value| / True Value] * 100
The absolute value (| |) ensures a positive percentage regardless of whether the measured value is higher or lower than the true value.
Solving More Complex Percentage Problems
While "What percentage is 2 of 6?" is a relatively simple problem, many real-world scenarios involve more complex percentage calculations. These might involve multiple steps, finding the original value given a percentage change, or working with compound percentages. Understanding the fundamental principles outlined above provides a strong base for tackling these more challenging problems. Practice is key to mastering percentage calculations and applying them effectively across various situations.
Conclusion: The Significance of Percentage Understanding
Understanding percentages is a vital life skill with numerous applications across various fields. This article has demonstrated how to calculate "What percentage is 2 of 6?" using several methods, highlighting the importance of understanding the underlying principles and their real-world applications. From financial planning to data analysis, mastering percentage calculations empowers individuals to interpret information more effectively and make informed decisions. Continuously practicing these calculations will enhance your proficiency and build confidence in tackling more complex percentage-related problems in the future. Remember that while calculators can assist, a firm grasp of the concepts remains crucial for problem-solving and critical thinking.
Latest Posts
Latest Posts
-
How Many 1 4 Teaspoons Are In 1 Teaspoon
Jul 02, 2025
-
How Many Tbsp In A Dry Ounce
Jul 02, 2025
-
How Do You Say Grandparents In Spanish
Jul 02, 2025
-
How Many Numbers Are Between 48 To 24
Jul 02, 2025
-
How Many Positions Are There In Sex
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 2 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.