What Percentage Is 20 Of 50
Kalali
Mar 13, 2025 · 5 min read
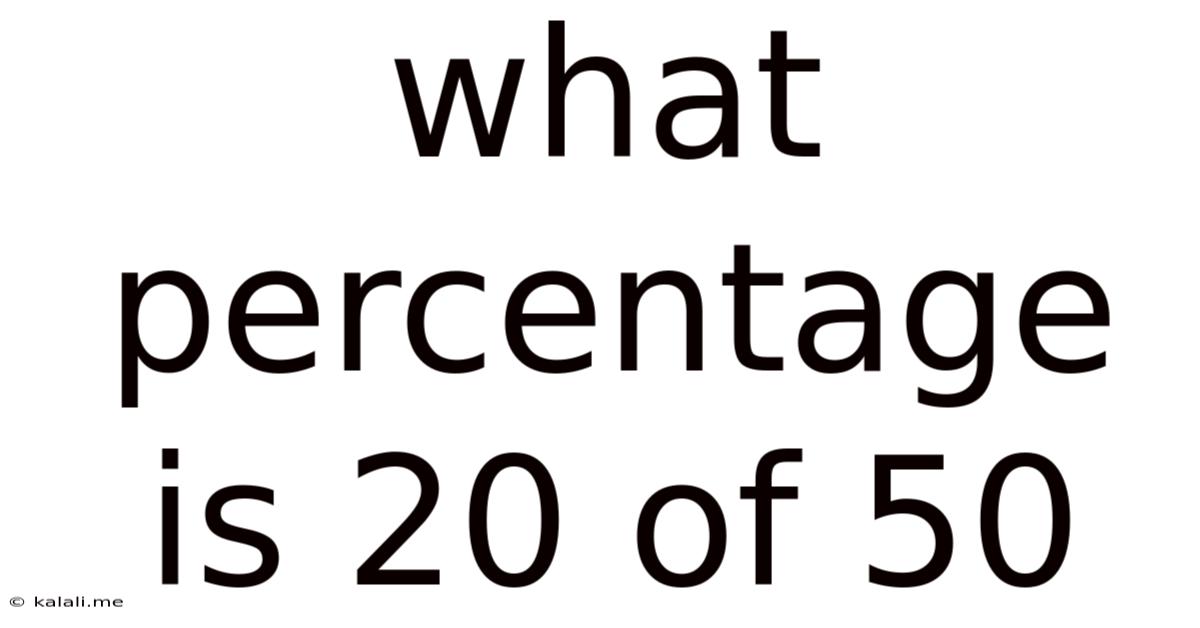
Table of Contents
What Percentage is 20 of 50? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the specifics of calculating what percentage 20 represents of 50, while also providing a broader understanding of percentage calculations and their practical applications.
Understanding Percentages: A Foundational Overview
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred," indicating a proportion relative to a whole. The symbol "%" is used to denote percentages. For example, 25% signifies 25 out of 100, or 25/100, which simplifies to 1/4.
Key Terms and Concepts
Before delving into the calculation, let's clarify some crucial terms:
- Base: The total amount or whole quantity to which a percentage refers. In our example, 50 is the base.
- Part: The specific amount or portion that represents a percentage of the base. In our example, 20 is the part.
- Percentage: The numerical value representing the ratio of the part to the base, expressed as a number out of 100. This is what we aim to calculate.
Calculating the Percentage: What Percentage is 20 of 50?
The calculation to determine what percentage 20 represents of 50 involves a straightforward formula:
(Part / Base) * 100 = Percentage
Let's plug in the values from our example:
(20 / 50) * 100 = Percentage
-
Divide the part by the base: 20 / 50 = 0.4
-
Multiply the result by 100: 0.4 * 100 = 40
Therefore, 20 is 40% of 50.
Different Methods for Calculating Percentages
While the above formula is the most common and straightforward method, there are alternative approaches that can be equally effective, especially depending on the complexity of the numbers involved or personal preference:
Method 1: Using Proportions
This method leverages the concept of proportions to solve for the unknown percentage. We can set up a proportion:
20/50 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
20 * 100 = 50 * x
2000 = 50x
x = 2000 / 50
x = 40
Therefore, x = 40%, confirming our earlier result.
Method 2: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100.
-
Convert the fraction to a decimal: 20/50 = 0.4
-
Multiply the decimal by 100: 0.4 * 100 = 40%
Practical Applications of Percentage Calculations
The ability to calculate percentages finds applications across a vast array of contexts, including:
1. Finance and Budgeting:
- Calculating interest: Determining the interest earned on savings accounts or the interest paid on loans.
- Analyzing investment returns: Assessing the profitability of investments and understanding growth rates.
- Budgeting and expense tracking: Determining the percentage of income spent on different categories.
- Sales tax calculations: Calculating the total cost of an item including sales tax.
- Discounts and markdowns: Calculating the final price of an item after a percentage discount.
2. Academic and Scientific Fields:
- Statistical analysis: Calculating percentages to represent data and trends in research.
- Scientific measurements: Expressing experimental results as percentages to show relative changes or proportions.
- Grading and assessment: Converting numerical scores into percentages for grading purposes.
3. Everyday Life:
- Tip calculations: Determining the appropriate tip amount at restaurants.
- Sales and discounts: Understanding the savings from promotional offers.
- Comparing prices: Determining the best value among different options.
- Understanding surveys and polls: Interpreting the results of surveys and polls expressed as percentages.
Advanced Percentage Calculations: Beyond the Basics
While the basic percentage calculation is relatively straightforward, several more complex scenarios may arise requiring a deeper understanding:
1. Calculating Percentage Increase or Decrease:
This involves determining the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100 = Percentage Change
For example, if a price increases from $50 to $60, the percentage increase is:
((60 - 50) / 50) * 100 = 20%
2. Finding the Original Value After a Percentage Change:
If you know the final value and the percentage change, you can work backward to find the original value. This requires some algebraic manipulation.
3. Calculating Percentage of a Percentage:
This involves finding a percentage of a percentage value. For instance, finding 10% of 20% of 100 would be calculated as follows:
(0.1 * 0.2 * 100) = 2
Mastering Percentage Calculations: Tips and Tricks
Here are some helpful tips and tricks to enhance your understanding and speed when performing percentage calculations:
- Memorize common percentages: Knowing the decimal equivalents of common percentages (e.g., 10% = 0.1, 25% = 0.25, 50% = 0.5, 75% = 0.75) can significantly speed up calculations.
- Use a calculator effectively: Calculators are valuable tools for percentage calculations, especially for more complex problems.
- Practice regularly: Consistent practice is key to mastering percentage calculations. Work through various examples to build your proficiency.
- Understand the context: Always carefully consider the context of the problem to ensure you're applying the correct method and interpreting the results correctly.
Conclusion: The Significance of Percentage Calculations
Understanding and performing percentage calculations is an invaluable skill with broad applications across diverse fields. From managing personal finances to interpreting scientific data, the ability to work with percentages is essential for making informed decisions and comprehending numerical information effectively. By mastering the fundamental principles outlined in this guide, you can confidently tackle various percentage-related problems and enhance your analytical abilities. Remember to practice consistently, and you will soon become proficient in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Is Dried Oregano A Pure Substance Or Mixture
Jul 04, 2025
-
What Is Fgteev Duddys Real Phone Number
Jul 04, 2025
-
What Are 2004 Pennies Worth Worlds Easyest Game
Jul 04, 2025
-
Who Did Alan Jackson Have An Affair With
Jul 04, 2025
-
How Much Is 500 Grams Of Ground Beef
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 20 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.