What Percentage Is 3 Of 12
Kalali
Mar 31, 2025 · 5 min read
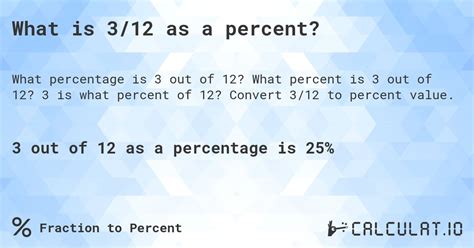
Table of Contents
What Percentage is 3 of 12? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. This article explores the calculation of "What percentage is 3 of 12?", delving into the method, variations, and real-world applications to solidify your understanding of percentage calculations.
Understanding the Fundamentals of Percentages
Before we dive into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Terms and Concepts
- Part: This represents the smaller number we're comparing (in our case, 3).
- Whole: This is the larger number to which the part is being compared (in our case, 12).
- Percentage: This is the result expressed as a number followed by the "%" symbol.
Calculating What Percentage 3 is of 12
There are several ways to calculate what percentage 3 represents of 12. Let's examine the most common methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
Substituting our values:
(3 / 12) * 100% = Percentage
Simplifying the fraction:
(1/4) * 100% = 25%
Therefore, 3 is 25% of 12.
Method 2: Using Proportions
We can also solve this using proportions. We set up a proportion where x represents the unknown percentage:
3/12 = x/100
To solve for x, we cross-multiply:
12x = 300
Now, divide both sides by 12:
x = 25
Therefore, 3 is 25% of 12.
Method 3: Decimal Conversion and Multiplication
Another approach involves converting the fraction to a decimal first and then multiplying by 100%:
3/12 = 0.25
0.25 * 100% = 25%
Again, we find that 3 is 25% of 12.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in a wide array of situations. Here are a few examples:
1. Financial Calculations:
- Interest Rates: Banks use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations allows you to compare interest rates from different institutions and make informed decisions.
- Discounts and Sales: Stores often advertise discounts as percentages. Knowing how to calculate percentages helps you determine the actual price after a discount is applied. For example, a 20% discount on a $50 item means a saving of $10 (20% of $50).
- Taxes: Taxes are usually expressed as percentages of income or the value of goods and services. Calculating tax amounts accurately is crucial for budgeting and financial planning.
- Investment Returns: Investors track the performance of their investments using percentage returns. Positive percentages indicate growth, while negative percentages reflect losses.
2. Academic Assessments:
- Grades: Grades in many educational systems are expressed as percentages, reflecting the proportion of correct answers or the overall performance on an assignment or exam. For example, a score of 15 out of 20 translates to 75%.
- Statistical Analysis: Percentages are essential in statistical analyses, helping researchers express and interpret data effectively. They allow for comparisons between groups and drawing meaningful conclusions.
3. Everyday Life:
- Tipping: People often tip restaurant servers a certain percentage of their bill. For instance, a 15% tip on a $40 meal amounts to $6.
- Shopping Comparisons: Comparing prices and values of products often involves calculating percentage differences to find the best deal.
- Nutrition Labels: Food labels often show the percentage of daily recommended values of various nutrients per serving. Understanding percentages allows for mindful eating and adherence to dietary recommendations.
- Sales Conversions: In sales and marketing, conversion rates are often expressed as percentages. This metric measures the effectiveness of marketing campaigns by assessing the proportion of visitors who take a desired action (e.g., making a purchase).
Variations and More Complex Percentage Problems
While the "What percentage is 3 of 12?" example is straightforward, percentage calculations can become more complex. Let's explore some variations:
1. Finding the Whole:
If you know the percentage and the part, you can calculate the whole. For instance, if 25% of a number is 3, what is the number?
We can use the formula:
(Part / Percentage) * 100 = Whole
(3 / 25) * 100 = 12
2. Finding the Part:
If you know the percentage and the whole, you can calculate the part. For example, what is 25% of 12?
We can use the formula:
(Percentage / 100) * Whole = Part
(25 / 100) * 12 = 3
3. Percentage Increase or Decrease:
These calculations involve determining the percentage change between two numbers. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100%
The formula for percentage decrease is:
[(Old Value - New Value) / Old Value] * 100%
For example, if a price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] * 100% = 20%
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The best way to master percentage calculations is through consistent practice. Start with simple problems and gradually work your way up to more complex ones.
- Use a Calculator: Don't hesitate to use a calculator for more complex calculations. This will save you time and reduce the risk of errors.
- Understand the Concepts: Focus on understanding the underlying concepts rather than simply memorizing formulas. This will help you approach various percentage problems more effectively.
- Visual Aids: Visual aids such as pie charts or bar graphs can be helpful in understanding and representing percentages.
- Online Resources: Numerous online resources, including calculators and tutorials, are available to assist you in learning and practicing percentage calculations.
Conclusion: The Significance of Percentage Understanding
The seemingly simple question "What percentage is 3 of 12?" reveals the fundamental importance of understanding percentage calculations. This skill is not only crucial for academic success but also essential for navigating everyday life, managing finances, and making informed decisions in various professional settings. By mastering these calculations and exploring their numerous applications, you equip yourself with a powerful tool for understanding and interpreting data, leading to better problem-solving and decision-making capabilities. From simple percentage calculations to more complex applications, a strong grasp of this concept is a valuable asset in many areas of life.
Latest Posts
Latest Posts
-
What Is 3 10 As A Decimal
Apr 02, 2025
-
0 25 Mole Of Mg Contains How Many Atoms
Apr 02, 2025
-
5 Lb Is How Many Oz
Apr 02, 2025
-
Cuanto Es 100 Mililitros En Onzas
Apr 02, 2025
-
10 Oz Is How Many Cups
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 3 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
