What Percentage Is 45 Out Of 50
Kalali
Mar 08, 2025 · 4 min read
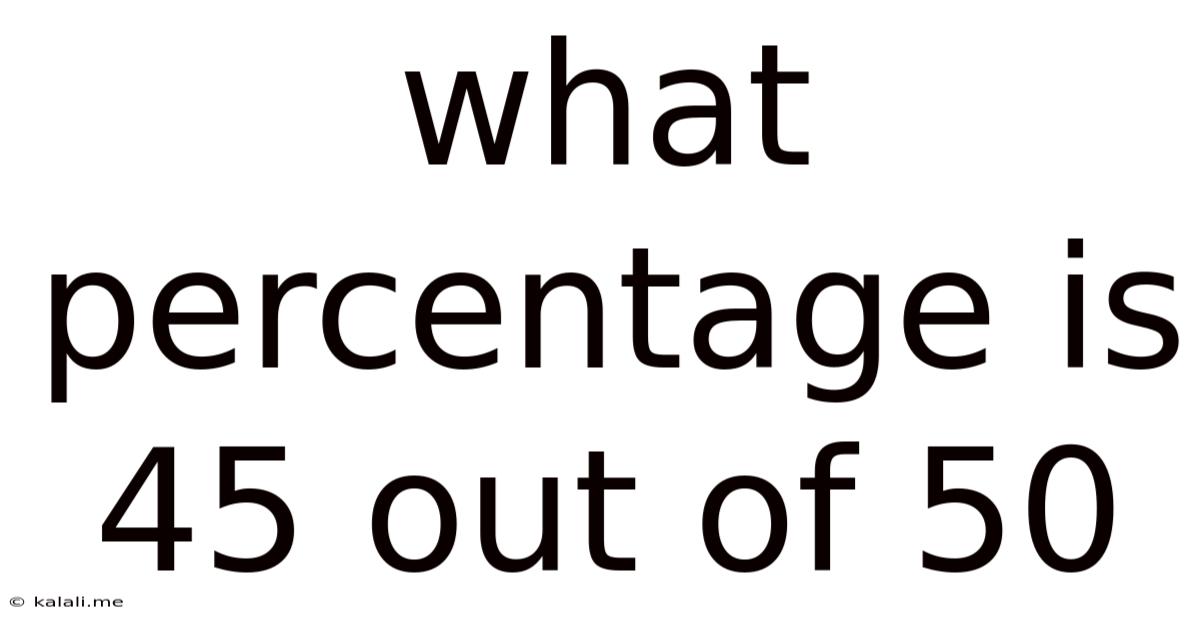
Table of Contents
What Percentage is 45 out of 50? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into calculating what percentage 45 is out of 50, explaining the process step-by-step, offering alternative methods, and exploring practical applications.
Understanding Percentages
Before we dive into the calculation, let's clarify the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Calculating What Percentage 45 is Out of 50
The most straightforward method for calculating this percentage involves converting the fraction 45/50 into a percentage. Here's a step-by-step breakdown:
Step 1: Express the Numbers as a Fraction
The problem "What percentage is 45 out of 50?" can be written as the fraction 45/50. This fraction represents the portion of 50 that 45 constitutes.
Step 2: Convert the Fraction to a Decimal
Divide the numerator (45) by the denominator (50):
45 ÷ 50 = 0.9
This decimal, 0.9, represents the proportion of 45 to 50.
Step 3: Convert the Decimal to a Percentage
Multiply the decimal by 100 and add the percentage symbol (%):
0.9 × 100 = 90%
Therefore, 45 is 90% of 50.
Alternative Methods for Percentage Calculation
While the above method is the most common, several alternative approaches can achieve the same result. These methods are useful for different scenarios and demonstrate the versatility of percentage calculations.
Method 1: Using Proportions
Proportions offer a powerful way to solve percentage problems. Set up a proportion:
x/100 = 45/50
Here, 'x' represents the percentage we're trying to find. Solve for 'x' by cross-multiplying:
50x = 4500
x = 4500 ÷ 50
x = 90
Therefore, 45 is 90% of 50.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 45 ÷ 50 and then multiply by 100 to obtain the percentage. This is a quick and efficient method, especially for more complex calculations.
Method 3: Mental Calculation (for simpler cases)
In simpler cases, like this one, a mental calculation might suffice. Recognizing that 45 is 9/10 of 50 (since 45/50 simplifies to 9/10), we can easily convert 9/10 to a percentage: (9/10) * 100% = 90%. This method relies on familiarity with common fractions and their percentage equivalents.
Practical Applications of Percentage Calculations
Understanding percentage calculations has broad practical implications. Here are a few examples:
-
Academic Performance: Calculating grades, test scores, and overall academic performance often involves percentages. For instance, scoring 45 out of 50 on a test translates to a 90% grade.
-
Financial Matters: Percentages are fundamental in finance. Calculating interest rates, discounts, taxes, and profit margins all rely on percentage calculations. A 90% discount on a product is a significant reduction in price.
-
Data Analysis: Interpreting statistical data often requires calculating percentages. For example, understanding the percentage of respondents who prefer a particular product in a survey helps to understand market trends.
-
Scientific Research: Many scientific fields utilize percentages for data representation and analysis. For example, determining the percentage of a specific compound in a mixture or the success rate of an experiment relies on these calculations.
-
Everyday Life: Even everyday activities involve percentages. Tip calculations in restaurants, sales tax calculation on purchases, and understanding discounts all require this knowledge.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, several common mistakes can lead to incorrect results.
-
Incorrect Order of Operations: Always ensure the division is performed before multiplying by 100.
-
Misinterpretation of the Question: Carefully read the question to understand which number represents the whole (denominator) and which represents the part (numerator).
-
Rounding Errors: When dealing with decimals, be mindful of rounding errors, especially in situations where precision is crucial.
-
Using the Wrong Formula: Make sure you’re applying the correct formula and steps for calculating the percentage.
Further Exploration of Percentages
Beyond the basic calculation of what percentage 45 is out of 50, exploring more complex percentage applications is beneficial. This can include:
-
Calculating percentage increase or decrease: Understanding how to calculate the percentage change between two values is valuable in many contexts.
-
Working with compound percentages: Compound percentages apply interest or growth repeatedly, leading to more significant changes over time.
-
Using percentages in various formulas: Percentages are integrated into numerous formulas across different disciplines.
-
Solving for unknown values: Learning to manipulate percentage equations to solve for unknown values is a powerful skill for problem-solving.
Conclusion
Determining what percentage 45 is out of 50, resulting in 90%, is a fundamental calculation with numerous real-world applications. Mastering percentage calculations enhances problem-solving skills across various disciplines, from academics and finance to everyday decision-making. Understanding the different methods, avoiding common errors, and exploring advanced applications will further solidify this vital mathematical concept. By practicing these techniques and understanding the underlying principles, you can confidently tackle percentage calculations in any context.
Latest Posts
Latest Posts
-
How Many Gallons In A 16x32 Pool
Jul 13, 2025
-
55 X 40 X 20 Cm Inches
Jul 13, 2025
-
If I Was Born In 1970 How Old Am I
Jul 13, 2025
-
Do The People On Naked And Afraid Get Paid
Jul 13, 2025
-
How Long Would It Take To Get To China
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 45 Out Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.