What Percentage Is 6 Out Of 7
Kalali
Apr 09, 2025 · 5 min read
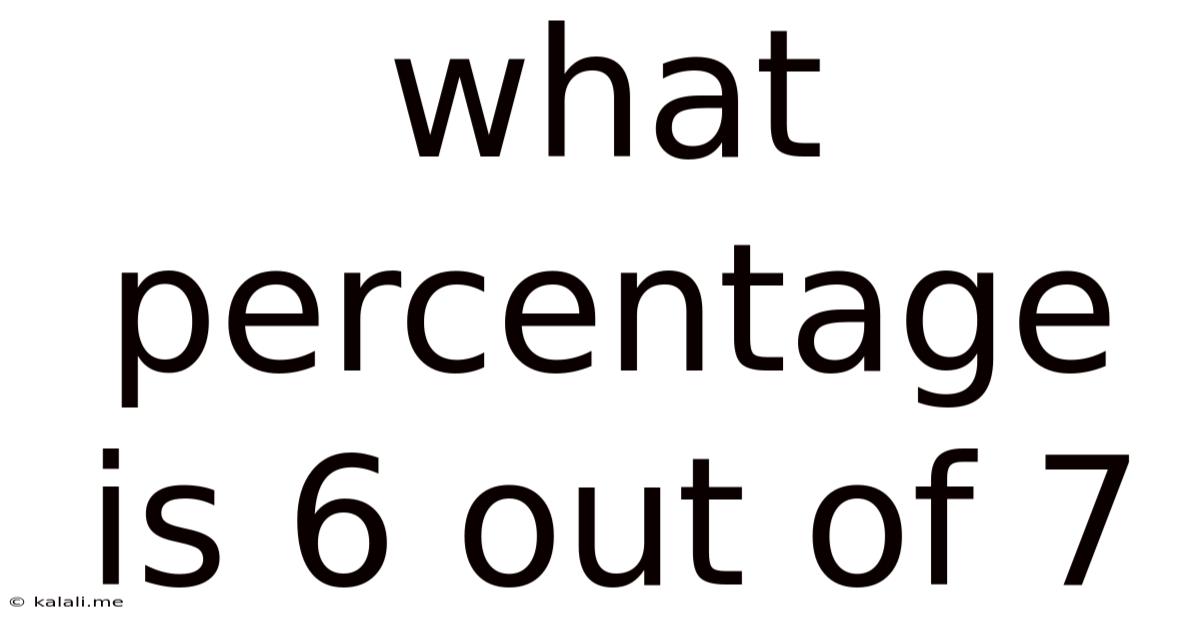
Table of Contents
What Percentage is 6 out of 7? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "What percentage is 6 out of 7?", opens the door to a world of practical applications and mathematical concepts. Understanding how to calculate percentages isn't just about solving school problems; it's a crucial skill for everyday life, from budgeting and shopping to understanding statistics and analyzing data. This article will not only answer the initial question but also explore the underlying principles of percentage calculations, delve into different methods of solving similar problems, and discuss real-world examples where this skill proves invaluable.
Meta Description: Learn how to calculate percentages with a detailed explanation of finding what percentage 6 out of 7 represents. This guide covers various methods, real-world applications, and related mathematical concepts.
Calculating the Percentage: The Fundamental Approach
The most straightforward way to determine what percentage 6 out of 7 represents involves using a simple formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 6 (the number we're considering as a portion of the whole)
- Whole: 7 (the total number)
Therefore, the calculation becomes:
(6 / 7) x 100% = 85.71% (approximately)
So, 6 out of 7 is approximately 85.71%. The slight decimal remainder is common in percentage calculations and can be rounded to the desired level of precision.
Understanding the Concept of Ratio and Proportion
The calculation above relies on the fundamental concept of ratios and proportions. A ratio is a comparison of two quantities, while a proportion expresses the equality of two ratios. In this case, the ratio of 6 to 7 can be expressed as 6:7 or 6/7. Converting this ratio to a percentage involves finding an equivalent ratio where the denominator is 100.
Alternative Methods for Calculating Percentages
While the formula (Part / Whole) x 100% is the most common and efficient method, several alternative approaches can be used, especially when dealing with more complex scenarios or when mental calculation is preferred.
-
Using Decimal Conversion: First, convert the fraction 6/7 to a decimal by dividing 6 by 7. This gives approximately 0.8571. Then, multiply the decimal by 100% to obtain the percentage: 0.8571 x 100% = 85.71%.
-
Cross-Multiplication: This method is particularly useful when dealing with proportions. If you know that x/100 = 6/7, you can cross-multiply: 7x = 600. Solving for x gives x = 600/7 ≈ 85.71. This is equivalent to our previous calculations.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the process. Simply input 6 ÷ 7 × 100 and press the "%" button. This will directly give the percentage result.
Real-World Applications of Percentage Calculations
The ability to calculate percentages has widespread applications in numerous fields:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. Understanding percentage changes in stock prices, for example, is crucial for informed investment decisions.
-
Retail and Sales: Determining discounts, sales tax, and markups are critical aspects of retail operations. Calculating percentage discounts (e.g., a 20% discount on a $100 item) is vital for both consumers and businesses.
-
Statistics and Data Analysis: Percentages are fundamental to expressing and interpreting data. Representing survey results, analyzing demographic trends, and understanding probabilities all involve percentage calculations. For example, expressing survey responses as percentages makes it easier to compare and understand the results.
-
Science and Engineering: Percentages are used extensively in scientific research and engineering design. Calculating error margins, expressing concentrations (e.g., percentage composition of a chemical compound), and analyzing experimental results frequently involve percentages.
-
Everyday Life: From calculating tips at restaurants to understanding nutritional information on food labels, percentages are a part of our daily routines. Knowing the percentage of fat or protein in food helps us make healthier choices.
Beyond the Basics: Percentage Increase and Decrease
Understanding percentages also involves calculating percentage increases and decreases. These calculations are essential in various contexts, such as tracking economic growth, analyzing population changes, or monitoring the performance of investments.
Percentage Increase: This calculates the proportional increase in a value over time. The formula is:
[(New Value - Old Value) / Old Value] x 100% = Percentage Increase
Percentage Decrease: This calculates the proportional decrease in a value over time. The formula is:
[(Old Value - New Value) / Old Value] x 100% = Percentage Decrease
For example, if a stock price rises from $50 to $60, the percentage increase is [(60-50)/50] x 100% = 20%.
Advanced Applications: Compound Interest and Growth Rates
More complex applications of percentages involve compound interest and exponential growth. Compound interest, where interest is calculated on both the principal amount and accumulated interest, is a fundamental concept in finance. Exponential growth, often modeled using exponential functions, describes situations where growth is proportional to the current value. Understanding these concepts requires a deeper understanding of mathematical principles beyond simple percentage calculations but builds upon the foundation of basic percentage understanding.
Conclusion: Mastering Percentages for Success
The seemingly simple question of "What percentage is 6 out of 7?" opens a door to a world of mathematical concepts and practical applications. Proficiently calculating percentages is not merely an academic exercise; it's a critical life skill with far-reaching implications. From managing personal finances to understanding complex data, a strong grasp of percentage calculations empowers individuals to make informed decisions and navigate various aspects of daily life with confidence. Mastering this fundamental skill provides a solid foundation for tackling more advanced mathematical problems and real-world challenges that involve proportions, ratios, and data analysis. By understanding the various methods and applications discussed in this article, you can significantly improve your numerical literacy and problem-solving abilities.
Latest Posts
Latest Posts
-
What Is 89 Cm In Inches
Apr 17, 2025
-
How Many Hours And Minutes Is 225 Minutes
Apr 17, 2025
-
What Is 190 Cm In Inches
Apr 17, 2025
-
What Is 3 Ounces In Cups
Apr 17, 2025
-
Cuanto Es 6 Metros En Pies
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 6 Out Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.