What Percentage Is 8 Out Of 30
Kalali
Apr 27, 2025 · 5 min read
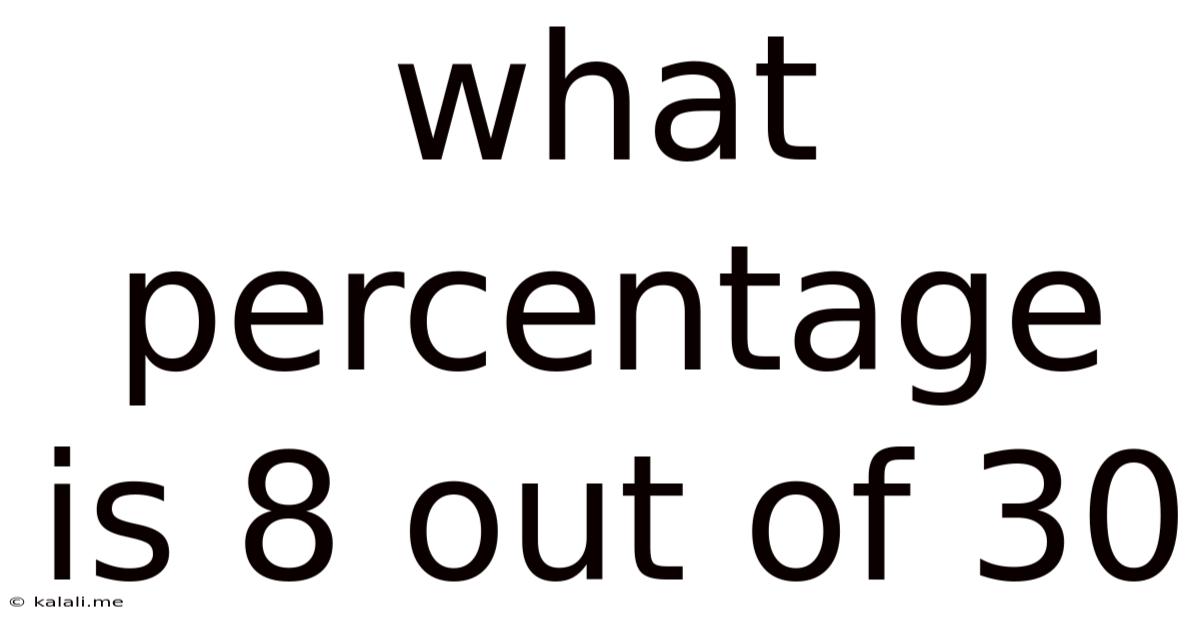
Table of Contents
What Percentage is 8 out of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts in a store to analyzing data in a professional setting. This comprehensive guide will delve into how to calculate what percentage 8 out of 30 represents, providing you with not only the answer but also a deeper understanding of the underlying principles and various methods for solving percentage problems. This article will cover different approaches, from the basic formula to more advanced techniques, ensuring you can confidently tackle similar calculations in the future. We’ll also explore practical applications and offer tips for improving your percentage calculation skills.
Meta Description: Learn how to calculate percentages effectively! This guide shows you how to determine what percentage 8 out of 30 represents, explaining multiple methods and offering practical examples. Master percentage calculations with ease.
Understanding the Basics of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentage is "%". Essentially, it expresses a proportion relative to a whole. For example, 50% means 50 out of 100, or one-half. The concept of percentages is widely used to represent proportions, changes, and ratios in various contexts.
Method 1: The Basic Percentage Formula
The most straightforward method to calculate the percentage is using the fundamental formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 8
- Whole: 30
Substituting these values into the formula:
(8 / 30) x 100% = 26.67% (approximately)
Therefore, 8 out of 30 is approximately 26.67%.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
- Convert the fraction to a decimal: Divide the part (8) by the whole (30): 8 / 30 = 0.266666...
- Multiply the decimal by 100%: 0.266666... x 100% = 26.67% (approximately)
Again, we arrive at the same answer: approximately 26.67%.
Method 3: Simplifying the Fraction First
Before applying the percentage formula, you can simplify the fraction to make the calculation easier.
- Find the greatest common divisor (GCD) of 8 and 30: The GCD of 8 and 30 is 2.
- Simplify the fraction: Divide both the numerator (8) and the denominator (30) by the GCD (2): 8/2 = 4 and 30/2 = 15. The simplified fraction is 4/15.
- Apply the percentage formula: (4 / 15) x 100% = 26.67% (approximately)
Understanding the Significance of Rounding
Notice that in all our calculations, we've obtained an approximate answer of 26.67%. This is because the decimal representation of 8/30 is a recurring decimal (0.26666...). Rounding is necessary to express the percentage in a manageable format. The level of rounding depends on the context. For instance, in financial calculations, you might need more precision, while in general estimations, rounding to one or two decimal places is often sufficient.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
- Sales and Discounts: Determining the discounted price of an item after a percentage discount.
- Finance: Calculating interest rates, profit margins, and tax amounts.
- Statistics and Data Analysis: Representing data as percentages for easier interpretation and comparison.
- Science: Expressing experimental results and uncertainties as percentages.
- Everyday Life: Calculating tips in restaurants, understanding survey results, and interpreting sports statistics.
Advanced Percentage Calculations: Finding the Whole or the Part
While we've focused on finding the percentage, percentage calculations can also involve finding the whole or the part given the percentage and either the part or the whole, respectively. Let's explore these scenarios:
Finding the Whole
Problem: 25% of a number is 10. What is the number?
Solution:
Let 'x' represent the whole number. We can set up an equation:
0.25x = 10
Solving for x:
x = 10 / 0.25 = 40
Therefore, the whole number is 40.
Finding the Part
Problem: What is 15% of 60?
Solution:
We can use the basic percentage formula:
(15/100) x 60 = 9
Therefore, 15% of 60 is 9.
Improving Your Percentage Calculation Skills
Here are some tips to enhance your ability to perform percentage calculations efficiently and accurately:
- Master the basic formula: Understand the underlying principles and be comfortable applying the (Part / Whole) x 100% formula.
- Practice regularly: The more you practice, the more proficient you'll become. Solve various percentage problems to build your confidence.
- Use calculators strategically: While manual calculations are important for understanding the process, utilize calculators for complex problems or when speed is essential.
- Learn mental math techniques: Develop shortcuts and tricks for calculating percentages mentally, especially for common percentages like 10%, 25%, and 50%.
- Check your work: Always review your calculations to ensure accuracy, especially in critical situations.
Conclusion: Mastering the Art of Percentage Calculations
Calculating percentages is a valuable skill that transcends academic settings and finds practical application in numerous daily situations. This comprehensive guide has provided a detailed explanation of how to determine what percentage 8 out of 30 represents, along with various methods and practical applications. By understanding the fundamental principles and practicing regularly, you can master the art of percentage calculations and confidently tackle a wide range of problems involving proportions and ratios. Remember that accuracy and understanding the underlying concepts are key to success in this essential mathematical skill. With consistent practice and the use of the techniques outlined here, you can easily and accurately calculate percentages in any scenario.
Latest Posts
Latest Posts
-
19 Is What Percent Of 10
Apr 27, 2025
-
How Long Is 300 Cm In Feet
Apr 27, 2025
-
How Many Inches Is 2 4 Cm
Apr 27, 2025
-
What Is 30 Percent Off 200
Apr 27, 2025
-
Which Statement Describes The Law Of Conservation Of Energy
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 8 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.