What Percentage Is 9 Out Of 13
Kalali
Aug 26, 2025 · 4 min read
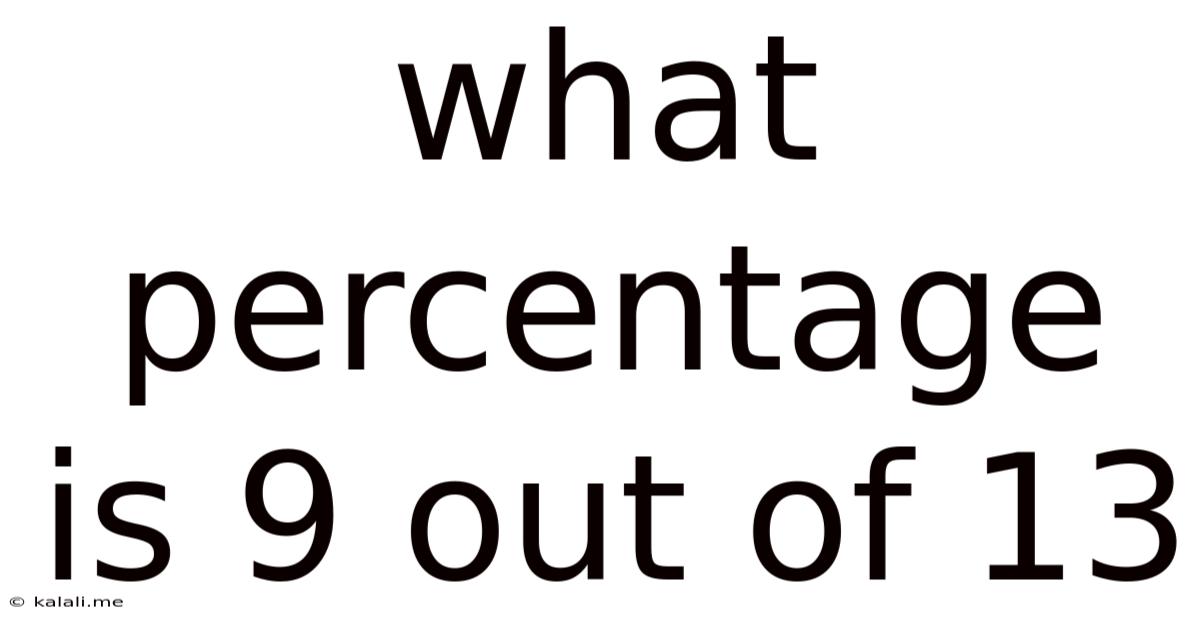
Table of Contents
What Percentage is 9 out of 13? A Comprehensive Guide to Percentage Calculations
Finding the percentage that 9 represents out of 13 might seem like a simple calculation, but understanding the underlying principles can unlock a world of practical applications in various fields. This comprehensive guide will delve into the intricacies of calculating percentages, exploring different methods, providing real-world examples, and addressing common misconceptions. We'll not only solve the specific problem of "What percentage is 9 out of 13?" but also equip you with the skills to tackle similar percentage problems confidently.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. It represents a portion or proportion of a whole. The symbol used to denote percentage is "%". For instance, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
The key to understanding percentages is the relationship between three core elements:
- The part: This is the specific amount you're interested in expressing as a percentage of the whole. In our case, the part is 9.
- The whole: This represents the total amount or the base value. In our case, the whole is 13.
- The percentage: This is the value we need to calculate, representing the part as a proportion of the whole, expressed as a percentage.
Method 1: Using the Formula
The most straightforward way to calculate a percentage is using the following formula:
(Part / Whole) x 100% = Percentage
Let's apply this to our problem:
(9 / 13) x 100% = Percentage
Calculating 9 divided by 13 gives us approximately 0.6923. Multiplying this by 100% yields:
0.6923 x 100% ≈ 69.23%
Therefore, 9 out of 13 is approximately 69.23%.
Method 2: Proportion Method
This method uses the concept of proportions to solve for the percentage. We set up a proportion where one ratio represents the part to the whole, and the other represents the percentage to 100.
Let 'x' represent the percentage we're trying to find:
9/13 = x/100
To solve for 'x', we cross-multiply:
13x = 900
x = 900/13
x ≈ 69.23
Therefore, again, 9 out of 13 is approximately 69.23%.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply enter 9 ÷ 13 and then multiply the result by 100. The calculator will automatically provide the percentage. This is the quickest method for most people.
Understanding the Result and Rounding
Our calculation resulted in approximately 69.23%. The decimal value ".23" indicates that 9 is slightly less than 70% of 13. The level of precision needed dictates how you round the result.
- For general purposes: Rounding to one decimal place (69.2%) is often sufficient.
- For scientific or financial applications: More decimal places might be necessary for accuracy.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life and professional fields. Here are a few examples:
- Finance: Calculating interest rates, discounts, tax amounts, profit margins, and returns on investment (ROI) all involve percentage calculations.
- Retail: Determining sale prices, calculating markups, and analyzing sales data heavily rely on percentages.
- Education: Evaluating exam scores, calculating grades, and tracking student progress all use percentages.
- Science: Representing experimental data, calculating statistical probabilities, and expressing concentrations often involve percentages.
- Sports: Calculating batting averages, winning percentages, and player statistics frequently utilizes percentage calculations.
Addressing Common Misconceptions
Several misconceptions surround percentage calculations. Let's address some of them:
-
Confusion with decimals and fractions: Remember that percentages, decimals, and fractions all represent the same underlying proportion. They are simply different ways of expressing the same value. You can easily convert between these formats.
-
Incorrect rounding: Rounding should be done thoughtfully, considering the required level of accuracy and avoiding unnecessary precision.
-
Improper application of the formula: Always ensure you correctly identify the "part" and the "whole" before applying the percentage formula. Misidentifying these elements will lead to incorrect results.
-
Assuming percentages are always whole numbers: Percentages can be decimal values, as demonstrated in our example (69.23%).
Beyond the Basics: More Complex Percentage Problems
While the "9 out of 13" problem is relatively straightforward, percentage calculations can become more complex. These might involve:
-
Calculating percentage increase or decrease: This involves comparing two values to find the percentage change between them. For example: What is the percentage increase from 10 to 15?
-
Finding the original value given a percentage and the result: For example: If 20% of a number is 12, what is the number?
-
Working with multiple percentages: For example: A price is discounted by 20%, and then an additional 10% discount is applied. What is the final price?
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with widespread applications. By understanding the fundamental concepts, formulas, and various calculation methods, you can confidently tackle various percentage-related problems. Remember to clearly identify the "part" and the "whole," use the appropriate formula, and consider the necessary level of precision when rounding your results. The ability to calculate percentages accurately and efficiently is a key element of numeracy, applicable across a wide array of personal and professional contexts. Whether you're analyzing financial statements, calculating grades, or simply understanding sales promotions, the ability to work with percentages will serve you well.
Latest Posts
Latest Posts
-
Sample Gun Permit Friend Character Reference Letter For Firearm
Aug 26, 2025
-
How Many Lines Is In A Pint
Aug 26, 2025
-
How Many Cups Is 16 Oz Of Cheese
Aug 26, 2025
-
Imagery Is Vivid Language That Appeals To The Readers
Aug 26, 2025
-
How Far Is 9 Miles In Minutes Driving
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 9 Out Of 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.