What Percentage Of 10 Is 6
Kalali
Apr 15, 2025 · 5 min read
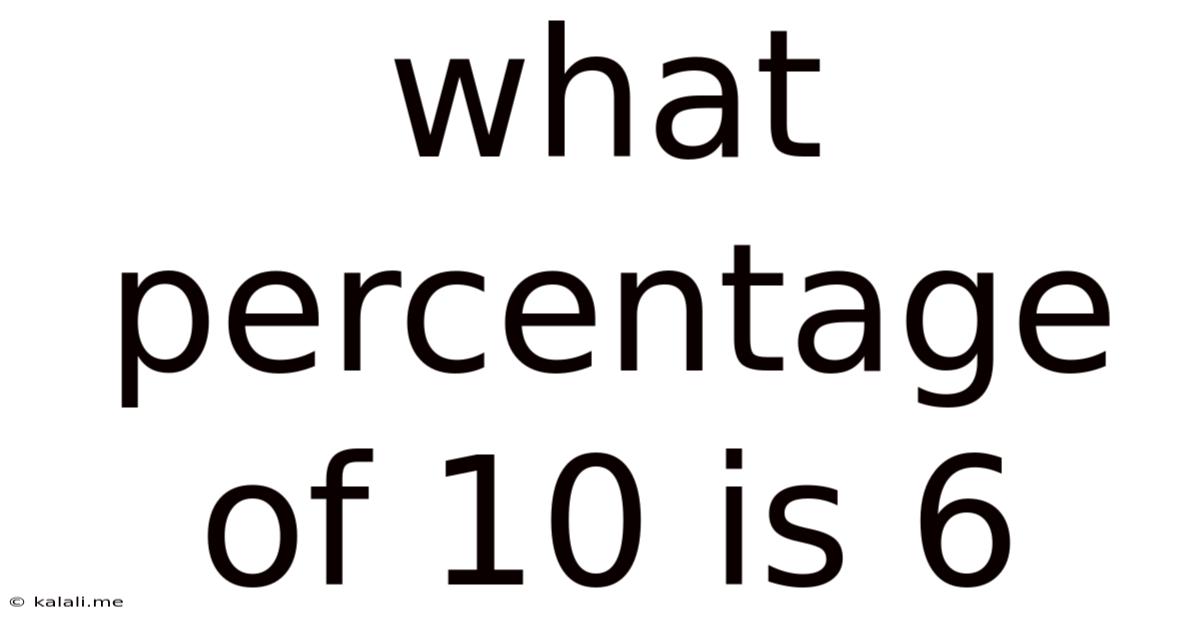
Table of Contents
What Percentage of 10 is 6? Understanding Percentage Calculations
This seemingly simple question, "What percentage of 10 is 6?", opens the door to a broader understanding of percentages and their applications in various fields. While the answer might seem immediately obvious to some, delving deeper reveals fundamental mathematical concepts and practical applications relevant to everyday life, finance, and various professional settings. This article will not only answer the question but also explore the underlying principles, provide step-by-step solutions, and illustrate practical examples to solidify your comprehension of percentage calculations.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percentage of 10 is 6. This guide covers the fundamentals of percentage calculations, provides step-by-step solutions, and explores practical applications.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 1% represents one out of every hundred parts. Understanding this fundamental concept is crucial to solving percentage problems.
Think of it like slicing a pizza. If you have a pizza cut into 100 equal slices, 1% would represent one single slice. 50% would represent 50 slices, and so on. This visual representation helps solidify the concept of percentages as parts of a whole.
Calculating "What Percentage of 10 is 6?"
Now, let's tackle the specific problem: determining what percentage of 10 is 6. There are several ways to approach this calculation:
Method 1: The Fraction Method
-
Express the relationship as a fraction: The problem can be represented as a fraction: 6/10. This fraction signifies that 6 is a part of the whole, which is 10.
-
Convert the fraction to a decimal: Divide the numerator (6) by the denominator (10): 6 ÷ 10 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.6 x 100 = 60
-
Add the percentage symbol: Therefore, 6 is 60% of 10.
Method 2: The Proportion Method
This method uses the concept of proportions, which states that two ratios are equal. We can set up a proportion to solve the problem:
- Let 'x' represent the unknown percentage.
- The proportion can be written as: x/100 = 6/10
To solve for 'x', we can cross-multiply:
-
10x = 600
-
x = 600 ÷ 10
-
x = 60
Therefore, 6 is 60% of 10.
Method 3: Using a Calculator
Most calculators have a percentage function. You can simply input the calculation as: (6/10) * 100 = 60%. This is the quickest method, but understanding the underlying principles is crucial for solving more complex percentage problems.
Practical Applications of Percentage Calculations
Percentage calculations are not just confined to mathematical exercises; they are indispensable tools in numerous real-world scenarios. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding compound interest, a concept that involves repeated percentage calculations, is vital for making informed financial decisions.
-
Retail: Discounts and sales are often expressed as percentages. Determining the final price after a discount requires calculating the percentage reduction. Similarly, sales tax is added as a percentage of the original price.
-
Science: Percentage calculations are used extensively in scientific research, particularly in statistical analysis and data interpretation. For example, calculating the percentage change in a population, the percentage error in an experiment, or the percentage composition of a substance.
-
Education: Grade calculations often involve percentages. The final grade is often a weighted average of individual assignment percentages.
-
Everyday Life: Many everyday scenarios involve percentages. Calculating tips in restaurants, determining the percentage of ingredients in recipes, or understanding sales statistics all involve percentage calculations.
-
Data Analysis: Representing data visually through charts and graphs often involves percentages. Pie charts, for instance, represent proportions of a whole using percentages.
Beyond the Basics: More Complex Percentage Problems
While the "What percentage of 10 is 6?" problem is relatively straightforward, percentage calculations can become more complex. Here are some examples of more challenging problems:
-
Finding the original value: If a discounted price is 80% of the original price and the discounted price is $40, what is the original price?
-
Calculating percentage increase or decrease: If a value increased from 50 to 60, what is the percentage increase? Conversely, if a value decreased from 100 to 80, what is the percentage decrease?
-
Working with multiple percentages: Calculating the final price after applying multiple discounts or taxes.
Solving these more advanced problems involves applying the same fundamental principles but with additional steps. Often, setting up equations and carefully applying the order of operations are crucial for accurate calculations.
Mastering Percentage Calculations: Tips and Tricks
-
Practice regularly: The best way to master percentage calculations is through consistent practice. Start with simple problems and gradually work your way towards more complex ones.
-
Understand the fundamentals: Ensure you have a solid grasp of fractions, decimals, and proportions, as these are the building blocks of percentage calculations.
-
Use visual aids: Visual aids like diagrams and charts can help you visualize percentage problems, making them easier to understand.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Utilize online resources: Many online resources offer practice problems and tutorials on percentage calculations.
Conclusion: The Importance of Percentage Understanding
In conclusion, the seemingly simple question, "What percentage of 10 is 6?", opens a door to a vast and practical world of percentage calculations. Mastering these calculations is essential for success in various academic, professional, and personal endeavors. Understanding the fundamental principles, employing different solution methods, and practicing regularly will equip you with the skills needed to confidently tackle percentage problems of varying complexities, ultimately enhancing your numerical literacy and problem-solving abilities. Remember, consistent practice and a thorough understanding of the underlying concepts are key to becoming proficient in this critical mathematical skill.
Latest Posts
Latest Posts
-
How Much Is 187 Ml In Ounces
Apr 18, 2025
-
Cuanto Es 5 6 Pies En Metros
Apr 18, 2025
-
How Many Inches Are In 180 Cm
Apr 18, 2025
-
What Is 11 25 As A Percent
Apr 18, 2025
-
How Much Feet Is 172 Cm
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 10 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.