What Percentage Of 16 Is 10
Kalali
Apr 17, 2025 · 5 min read
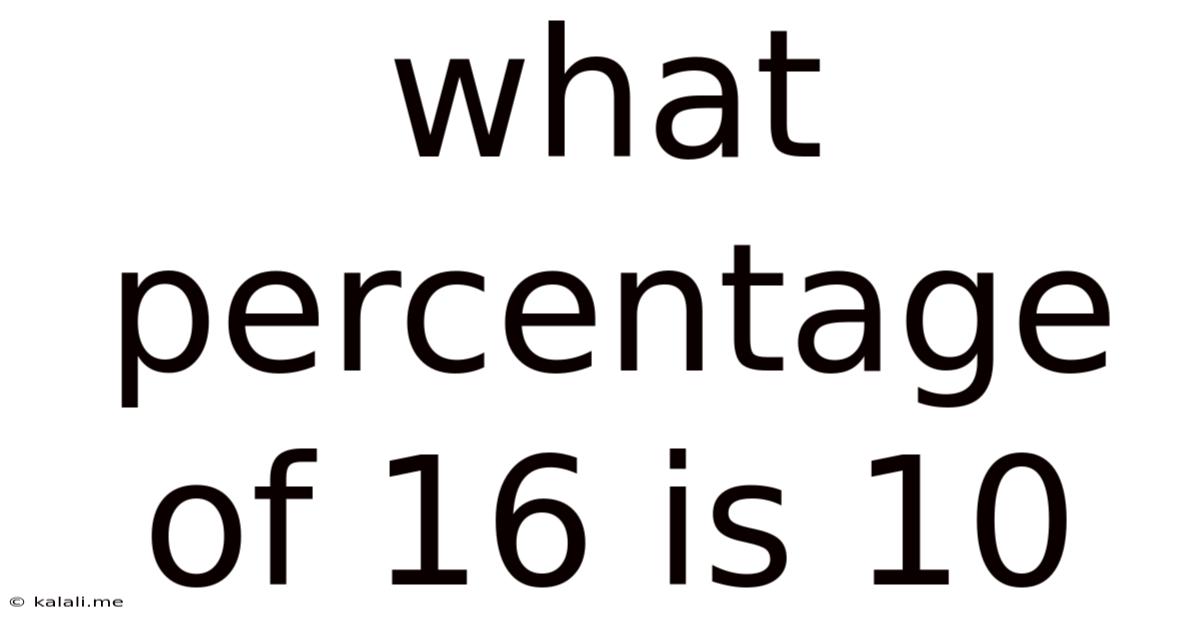
Table of Contents
What Percentage of 16 is 10? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percentage of 16 is 10?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and how to approach similar problems with confidence. While the answer itself is straightforward, understanding the underlying principles allows you to tackle more complex percentage problems and apply this knowledge to various fields, from finance and statistics to cooking and shopping. This article will provide a comprehensive guide, not just to solving this specific problem but to mastering percentage calculations in general.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percentage of 16 is 10. This guide covers various methods, real-world applications, and helps you master percentage calculations.
Understanding Percentages: The Basics
Before diving into the specifics of our problem, let's establish a solid foundation in understanding percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Percentages are incredibly useful for representing proportions and making comparisons. They are widely used in various contexts, including:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and more.
- Statistics: Representing data in charts and graphs, analyzing survey results, and understanding probabilities.
- Everyday life: Calculating tips, sales tax, discounts at stores, and understanding nutritional information on food labels.
Method 1: Using Proportions to Solve "What Percentage of 16 is 10?"
The most fundamental approach to solving percentage problems involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In our case, we can set up the proportion as follows:
- Part / Whole = Percentage / 100
Here, the "part" is 10 (the number we're trying to express as a percentage), and the "whole" is 16 (the total amount). Let's represent the unknown percentage as 'x':
- 10 / 16 = x / 100
To solve for 'x', we can cross-multiply:
- 10 * 100 = 16 * x
- 1000 = 16x
- x = 1000 / 16
- x = 62.5
Therefore, 10 is 62.5% of 16.
Method 2: Using Decimal Conversion
Another effective method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage. This method is often quicker for simpler problems:
- Form the fraction: Represent the problem as a fraction: 10/16
- Convert to a decimal: Divide 10 by 16: 10 ÷ 16 = 0.625
- Multiply by 100: Multiply the decimal by 100 to convert it to a percentage: 0.625 * 100 = 62.5%
This method confirms our previous result: 10 is 62.5% of 16.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function (%) that directly calculates percentages. The steps would generally involve:
- Divide: Divide the part (10) by the whole (16): 10 ÷ 16
- Multiply by 100: Multiply the result by 100. Some calculators will automatically display the result as a percentage; others might require you to manually add the "%" symbol.
This method offers speed and accuracy, especially for more complex problems.
Real-World Applications: Percentage Calculations in Everyday Life
Understanding percentage calculations is crucial for navigating various aspects of daily life. Here are some examples:
- Shopping: Calculating discounts. If a $20 item is discounted by 25%, you'd calculate 25% of $20 ($5) and subtract it from the original price ($15).
- Finance: Calculating interest earned on savings accounts or interest paid on loans.
- Taxes: Determining the amount of sales tax or income tax owed.
- Tipping: Calculating a gratuity at a restaurant. A 15% tip on a $50 meal would be 15% of $50 ($7.50).
- Nutrition: Understanding the percentage of daily recommended values for nutrients in food products.
- Surveys and polls: Interpreting data presented as percentages to understand public opinion.
- Sports: Calculating batting averages, win percentages, and other statistics.
Beyond the Basics: Tackling More Complex Percentage Problems
While the "what percentage of 16 is 10?" problem is relatively straightforward, mastering percentage calculations also means being able to solve more complex problems. These can involve:
- Finding the whole when you know the part and the percentage: For example, "15% of what number is 3?"
- Finding the part when you know the whole and the percentage: For example, "What is 30% of 80?"
- Calculating percentage increase or decrease: For example, finding the percentage increase from 50 to 60, or the percentage decrease from 100 to 80.
- Working with compound percentages: Calculating percentages over multiple periods, taking into account previous percentage changes.
These more advanced problems often require a more systematic approach, often involving algebraic equations or the use of more sophisticated calculation tools. However, the fundamental principles of ratios and proportions remain the cornerstone of solving these problems.
Practical Tips for Mastering Percentage Calculations
Here are some helpful tips to enhance your skills in percentage calculations:
- Practice regularly: The more you practice, the more comfortable and confident you will become. Try solving various percentage problems from different contexts.
- Use different methods: Experiment with different methods (proportions, decimal conversion, calculators) to find the approach you find most efficient and intuitive.
- Break down complex problems: Divide complex problems into smaller, more manageable steps.
- Check your work: Always double-check your answers to ensure accuracy.
- Use online resources: Many websites and apps offer practice problems and tutorials on percentage calculations.
Conclusion: The Power of Percentage Understanding
The question "What percentage of 16 is 10?" serves as a springboard to understanding the broader world of percentage calculations. While the answer (62.5%) is relatively simple to obtain, the underlying principles and their applications are far-reaching. By mastering percentage calculations, you equip yourself with a valuable skill set applicable across numerous areas of life, from managing personal finances to interpreting data and making informed decisions. Remember that consistent practice and a solid understanding of the fundamental principles are key to becoming proficient in this essential mathematical skill. The more you engage with percentage problems, the more intuitive and effortless the calculations will become.
Latest Posts
Latest Posts
-
What 2 Planets Have No Moons
Apr 19, 2025
-
What Is 5 7 As A Decimal
Apr 19, 2025
-
20 Of What Number Is 16
Apr 19, 2025
-
How Long Is 75cm In Inches
Apr 19, 2025
-
Cuanto Es 30 Pulgadas En Metros
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 16 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.