What Percentage Of 18 Is 3
Kalali
Apr 18, 2025 · 5 min read
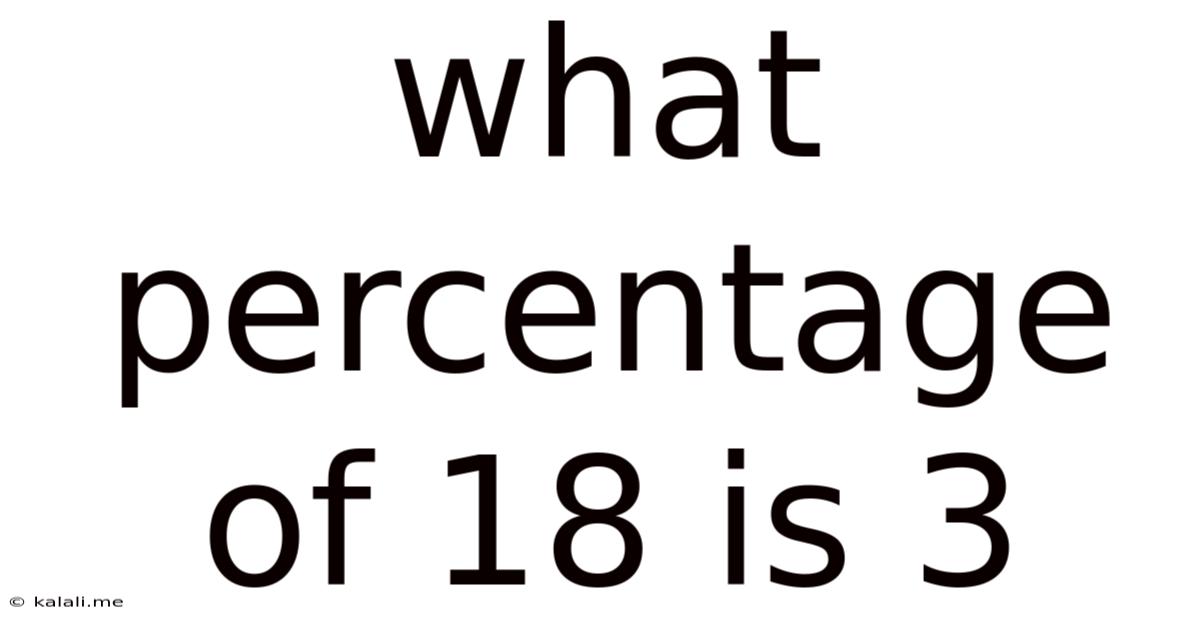
Table of Contents
What Percentage of 18 is 3? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percentage of 18 is 3?", opens the door to a broader understanding of percentage calculations, their applications in various fields, and even the underlying mathematical principles. While the answer itself is straightforward, exploring the how and why behind the calculation unlocks valuable skills applicable to numerous real-world scenarios, from calculating discounts and tax rates to understanding statistical data and financial reports. This article will not only provide the solution but also delve into the methodology, alternative approaches, and practical applications of percentage calculations.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be easily converted into a decimal or a fraction. For example, 50% is equivalent to 50/100 (as a fraction) or 0.5 (as a decimal). This understanding is crucial for solving percentage problems.
Method 1: The Direct Approach – Solving for the Percentage
The most straightforward way to determine what percentage of 18 is 3 is to use the following formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 3 (the value we're comparing)
- Whole: 18 (the total value)
Substituting these values into the formula, we get:
(3 / 18) * 100 = Percentage
(1/6) * 100 = 16.67%
Therefore, 3 is 16.67% of 18. We round to two decimal places for practicality and common usage in percentage reporting.
Method 2: Using Proportions – A Visual Approach
Proportions offer a visual and intuitive way to solve percentage problems. We can set up a proportion as follows:
3 / 18 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
3 * 100 = 18 * x
300 = 18x
x = 300 / 18
x = 16.67
Again, this confirms that 3 is 16.67% of 18. This method is particularly helpful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Equivalents – A Flexible Approach
We can also solve this problem by first converting the percentage to its decimal equivalent. We know that we're looking for a fraction of 18 that equals 3. Let's represent the unknown percentage as 'x' as a decimal:
18 * x = 3
Solving for 'x':
x = 3 / 18
x = 0.1667
To convert this decimal back into a percentage, we multiply by 100:
0.1667 * 100 = 16.67%
Practical Applications: Where Percentage Calculations Matter
Understanding percentage calculations extends far beyond simple mathematical exercises. They're integral to numerous real-world applications, including:
1. Finance and Budgeting:
- Calculating interest rates: Understanding percentages is vital for comprehending interest earned on savings accounts or interest paid on loans.
- Analyzing financial statements: Financial reports heavily rely on percentages to represent ratios, profit margins, and growth rates. For example, the percentage change in revenue year-over-year is crucial for investors and stakeholders.
- Determining discounts and sales tax: Calculating discounts offered during sales or adding sales tax to a purchase price involves direct percentage calculations. Understanding these allows consumers to make informed purchasing decisions.
2. Statistics and Data Analysis:
- Interpreting survey results: Percentages are commonly used to represent responses in surveys and polls, providing a concise summary of the data. For example, what percentage of respondents favored a particular candidate or product?
- Understanding probability and risk: Percentages are used to express the likelihood of events occurring, which is fundamental in risk assessment, insurance, and investment strategies.
- Analyzing trends and patterns: Percentages are used to showcase trends in data, such as population growth, unemployment rates, or market share changes.
3. Science and Engineering:
- Calculating efficiency: In engineering and manufacturing, efficiency is often expressed as a percentage, indicating how effectively a system or process utilizes resources.
- Measuring concentration: In chemistry, the concentration of a solution is often expressed as a percentage, such as percentage weight or volume.
- Representing error margins: In scientific experiments, error margins are often represented as percentages to indicate the accuracy and precision of measurements.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants commonly involves percentage calculations.
- Understanding discounts: Determining the actual price of an item after a percentage discount is essential for cost-effective shopping.
- Tracking progress: Percentages can be used to track progress towards goals, such as completing a project or achieving a fitness objective.
Beyond the Basics: More Complex Percentage Problems
While this article focuses on a fundamental percentage calculation, many problems involve multiple steps or require a deeper understanding of percentage changes, percentage points, and compound interest.
Percentage Increase and Decrease: These calculations are essential for analyzing changes over time. For example, if a company's revenue increased from 100 to 120, the percentage increase would be calculated as:
((120 - 100) / 100) * 100 = 20%
Percentage Points: This term is often confused with percentage change. A percentage point represents the arithmetic difference between two percentages. For instance, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, not 60%.
Compound Interest: This involves calculating interest not only on the principal amount but also on accumulated interest from previous periods. This exponential growth makes compound interest a powerful tool for investment, but also a significant factor in debt accumulation.
Conclusion:
The seemingly simple question of "What percentage of 18 is 3?" serves as a gateway to a much wider world of percentage calculations. Understanding the fundamental principles, various methods for solving percentage problems, and their practical applications empowers individuals to confidently tackle various quantitative challenges in their personal and professional lives. Mastering percentage calculations is an invaluable skill applicable across numerous disciplines, from finance and statistics to science and everyday decision-making. By understanding the underlying concepts and applying the appropriate methods, anyone can become proficient in using percentages to analyze data, make informed choices, and understand the world around them more effectively.
Latest Posts
Latest Posts
-
Waves Interact With And Other
Apr 22, 2025
-
154 Cm Is How Many Feet
Apr 22, 2025
-
What Is 2 5 As A Percentage
Apr 22, 2025
-
What Is 50 Cm In Feet
Apr 22, 2025
-
How Many Mm Are In 25 Cm
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 18 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.