What Percentage Of 25 Is 4
Kalali
Apr 15, 2025 · 5 min read
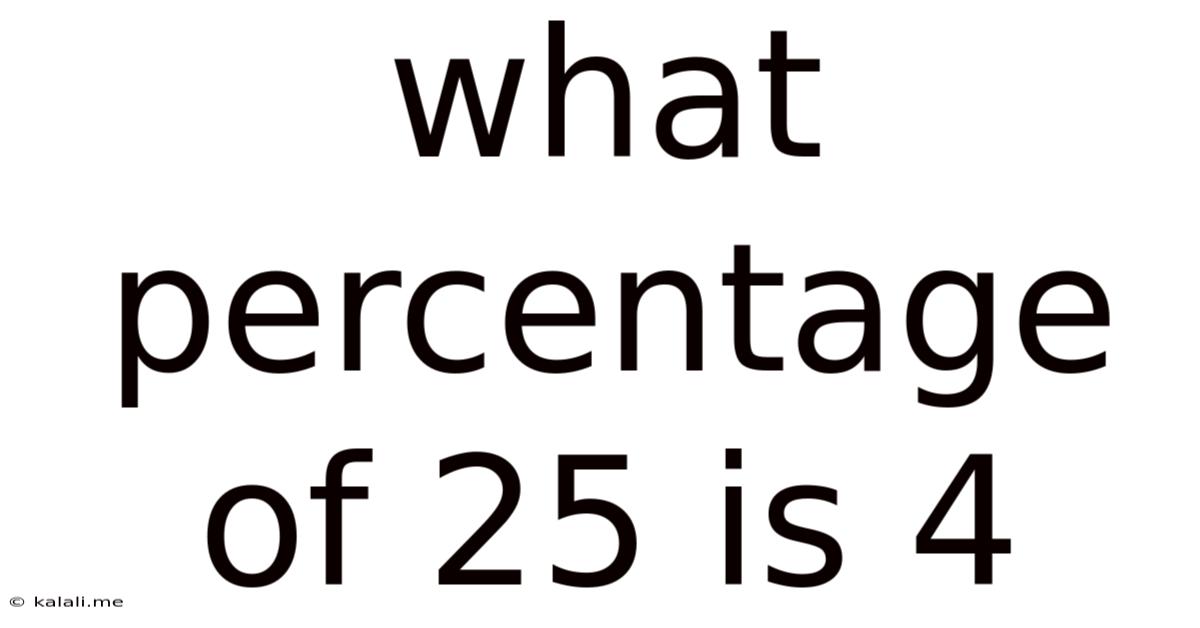
Table of Contents
What Percentage of 25 is 4? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percentage of 25 is 4?" – opens the door to a broader understanding of percentage calculations, their applications in various fields, and even some interesting mathematical concepts. This article will not only answer the question directly but will also explore the underlying principles, provide multiple solution methods, and showcase real-world examples where such calculations are crucial. Understanding percentages is fundamental to interpreting data, making financial decisions, and comprehending numerous everyday situations.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percentage 4 represents of 25. This guide covers multiple methods, real-world applications, and explores the underlying mathematical principles.
The Direct Answer and the Basic Formula
The answer to "What percentage of 25 is 4?" is 16%.
This is derived from the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
(4 / 25) x 100% = 16%
This simple formula forms the bedrock of all percentage calculations. Understanding how to manipulate this formula is key to solving a wide range of percentage problems.
Different Approaches to Solving the Problem
While the basic formula provides a straightforward solution, there are other approaches that can be equally effective, especially when dealing with more complex percentage problems. Let's explore a few:
1. Using Proportions:
Percentage problems can often be solved using proportions. We can set up a proportion as follows:
4/25 = x/100
Here, 'x' represents the percentage we're trying to find. By cross-multiplying, we get:
25x = 400
Solving for x:
x = 400 / 25 = 16
Therefore, x = 16%, confirming our initial answer. This method is particularly helpful when visualizing the relationship between the parts and the whole.
2. Using Decimal Conversion:
Another approach involves converting the fraction 4/25 into a decimal and then multiplying by 100%.
4/25 = 0.16
0.16 x 100% = 16%
This method is efficient and relies on basic decimal arithmetic, making it a readily accessible approach for many.
3. Using a Calculator:
Modern calculators are equipped to handle percentage calculations directly. Simply input "4 ÷ 25 × 100" and the calculator will return the answer, 16. While this method is convenient, it's crucial to understand the underlying principles to apply these calculations effectively in situations where a calculator might not be readily available.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life, impacting various aspects of our personal and professional lives. Here are a few examples:
-
Finance: Calculating interest rates, discounts, tax percentages, and profit margins all rely heavily on percentage calculations. For example, understanding what percentage of your income goes towards taxes is crucial for financial planning. Similarly, calculating the interest earned on a savings account or the interest paid on a loan requires a strong grasp of percentage calculations. Determining the discount on a sale item, for instance, a 20% discount on a $50 item, requires understanding percentage reductions.
-
Statistics and Data Analysis: Percentages are indispensable tools in statistics. Representing data as percentages allows for easy comparison and interpretation. For instance, analyzing survey results, understanding market share, or interpreting economic indicators often involves expressing data as percentages. Understanding that 60% of respondents prefer a particular product provides a clear, concise understanding of the preference distribution.
-
Science and Engineering: Percentages are used extensively in scientific and engineering calculations. For example, calculating the efficiency of a machine, the concentration of a solution, or the error rate in a measurement often involves expressing results as percentages. In chemistry, understanding the percentage composition of a compound is fundamental.
-
Education: Grading systems, exam scores, and performance metrics in education are often expressed as percentages, facilitating easy comparison and evaluation of student performance. Understanding a student's 85% score on an exam provides immediate context to their performance relative to the total possible marks.
-
Everyday Life: Calculating tips in restaurants, understanding sales tax, figuring out the percentage of completion of a project, or comparing prices all involve percentage calculations. Determining the best value for money often requires comparing percentages of discounts or unit prices.
Expanding on the Concept: Percentage Increase and Decrease
The problem "What percentage of 25 is 4?" implicitly involves a percentage decrease. If we started with 25 and ended up with 21 (25 - 4), we could calculate the percentage decrease as follows:
(Decrease / Original Value) x 100% = Percentage Decrease
(4 / 25) x 100% = 16%
Conversely, we can also calculate percentage increases. For example, if a value increases from 25 to 29 (an increase of 4), the percentage increase is:
(Increase / Original Value) x 100% = Percentage Increase
(4 / 25) x 100% = 16%
Addressing Potential Confusions and Common Mistakes
One common mistake in percentage calculations is confusing the "part" and the "whole" in the formula. Always clearly identify which value represents the part and which represents the whole. Another frequent error is incorrectly applying the percentage increase/decrease formula, particularly when dealing with successive increases or decreases.
Conclusion: The Power and Versatility of Percentage Calculations
This in-depth exploration of the seemingly simple question – "What percentage of 25 is 4?" – has revealed the fundamental importance and wide-ranging applications of percentage calculations. Mastering percentage calculations is not just a matter of rote memorization; it's about understanding the underlying mathematical principles and their practical applications in various contexts. From financial decisions to scientific analyses, the ability to confidently and accurately calculate and interpret percentages is a valuable skill with significant real-world implications. By understanding the multiple methods available and being aware of potential pitfalls, you can confidently tackle a wide range of percentage problems and leverage this knowledge to make informed decisions in various aspects of your life.
Latest Posts
Latest Posts
-
25 Is 50 Percent Of What
Apr 16, 2025
-
What Is The Least Common Denominator Of 8 And 9
Apr 16, 2025
-
1 To The Power Of 5
Apr 16, 2025
-
How Many Hours Is 190 Minutes
Apr 16, 2025
-
Cuanto Es 60 Milimetros En Pulgadas
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 25 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.