What Percentage Of 30 Is 40
Kalali
Apr 04, 2025 · 4 min read
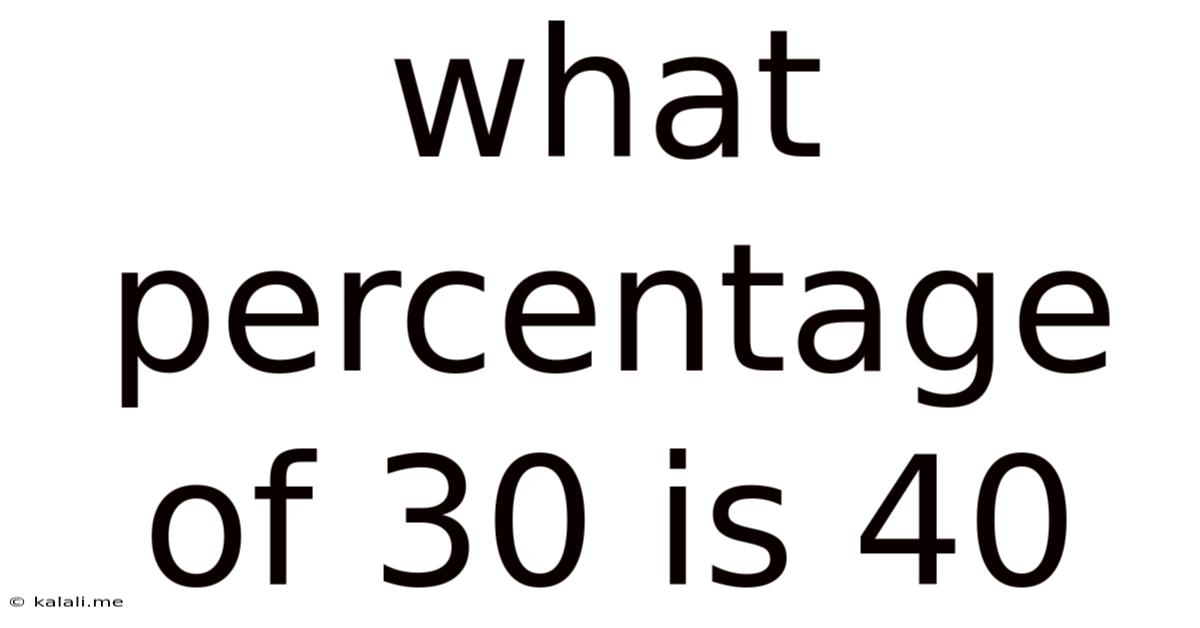
Table of Contents
What Percentage of 30 is 40? Understanding Percentage Calculations
This seemingly simple question, "What percentage of 30 is 40?", delves into a fundamental mathematical concept crucial for various applications in everyday life and professional fields. While the answer might initially seem counterintuitive (a percentage greater than 100%), understanding the underlying principles is key to mastering percentage calculations. This article will not only answer the question but also equip you with the knowledge to tackle similar problems, explaining the methodology, exploring practical examples, and even touching on advanced applications.
Deconstructing the Problem: Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. The percentage sign (%) is a shorthand way of representing this fraction.
The core of percentage problems involves finding the relationship between three quantities:
- The Part: This is the portion we're interested in. In our problem, "What percentage of 30 is 40?", the part is 40.
- The Whole: This represents the total amount. In our problem, the whole is 30.
- The Percentage: This is the fraction (expressed as a percentage) that represents the relationship between the part and the whole. This is what we need to find.
Calculating the Percentage: The Step-by-Step Approach
The calculation to determine what percentage of 30 is 40 involves a straightforward formula:
(Part / Whole) * 100% = Percentage
Let's plug in the values from our problem:
(40 / 30) * 100% = Percentage
This simplifies to:
(4/3) * 100% = 133.33%
Therefore, 40 is 133.33% of 30.
Why is the Percentage Greater Than 100%?
The result of 133.33% might initially seem surprising. It's important to remember that percentages can be greater than 100%. This simply indicates that the "part" (40) is larger than the "whole" (30). This often occurs in scenarios involving growth, increase, or situations where a value exceeds the initial amount.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios, including:
1. Finance and Business:
- Profit margins: Calculating profit as a percentage of revenue.
- Interest rates: Determining the interest earned or paid on loans and investments.
- Sales tax: Calculating the tax amount on purchases.
- Discounts: Determining the price reduction based on a percentage discount.
- Investment returns: Assessing the percentage growth or loss of investments.
2. Data Analysis and Statistics:
- Data representation: Visualizing data using percentages in charts and graphs.
- Statistical analysis: Calculating percentages for various statistical measures.
- Population growth: Analyzing population changes over time as percentages.
3. Everyday Life:
- Tip calculations: Determining the appropriate tip amount in restaurants.
- Sales and discounts: Understanding price reductions in stores.
- Recipe adjustments: Scaling recipes up or down by a certain percentage.
- Grading systems: Understanding scores and grades expressed as percentages.
More Complex Percentage Problems: Variations and Solutions
While the initial problem was relatively straightforward, let's explore some variations and delve into more complex scenarios:
1. Finding the Part:
Problem: 25% of a number is 15. What is the number?
Solution: We can set up an equation:
0.25 * x = 15
Solving for x:
x = 15 / 0.25 = 60
Therefore, the number is 60.
2. Finding the Whole:
Problem: 120 is 150% of what number?
Solution: We can set up an equation:
120 = 1.5 * x
Solving for x:
x = 120 / 1.5 = 80
Therefore, 120 is 150% of 80.
3. Percentage Increase/Decrease:
Problem: A price increased from $50 to $60. What is the percentage increase?
Solution:
- Find the difference: $60 - $50 = $10
- Divide the difference by the original amount: $10 / $50 = 0.2
- Multiply by 100%: 0.2 * 100% = 20%
The price increased by 20%.
Advanced Applications: Compound Interest and Exponential Growth
Percentage calculations are fundamental to understanding compound interest and exponential growth. Compound interest, where interest is earned on both the principal amount and accumulated interest, is a powerful tool for wealth building. Exponential growth, where the rate of growth is proportional to the current value, describes many phenomena in nature and finance. Understanding how percentages are used in these contexts is crucial for making informed financial decisions.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental skill with widespread applications across various domains. From everyday financial transactions to advanced mathematical modeling, the ability to perform accurate percentage calculations is invaluable. By grasping the underlying principles and practicing different problem types, you can significantly improve your quantitative reasoning skills and make informed decisions in various aspects of your life. This article has provided a comprehensive overview, equipping you with the tools and knowledge to confidently tackle percentage-related problems and excel in any field requiring these crucial calculations. Remember that practice is key—the more you work with percentages, the more intuitive and effortless the calculations will become.
Latest Posts
Latest Posts
-
How Many Cm Is 76 Inches
Apr 11, 2025
-
How Long Do Hurricanes Normally Lsat
Apr 11, 2025
-
What Is 32 In In Feet
Apr 11, 2025
-
How Many Cups In 64 Fluid Ounces
Apr 11, 2025
-
Which Property Do Metalloids Share With Nonmetals
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 30 Is 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.