What Percentage Of 5 Is 3
Kalali
Mar 09, 2025 · 4 min read
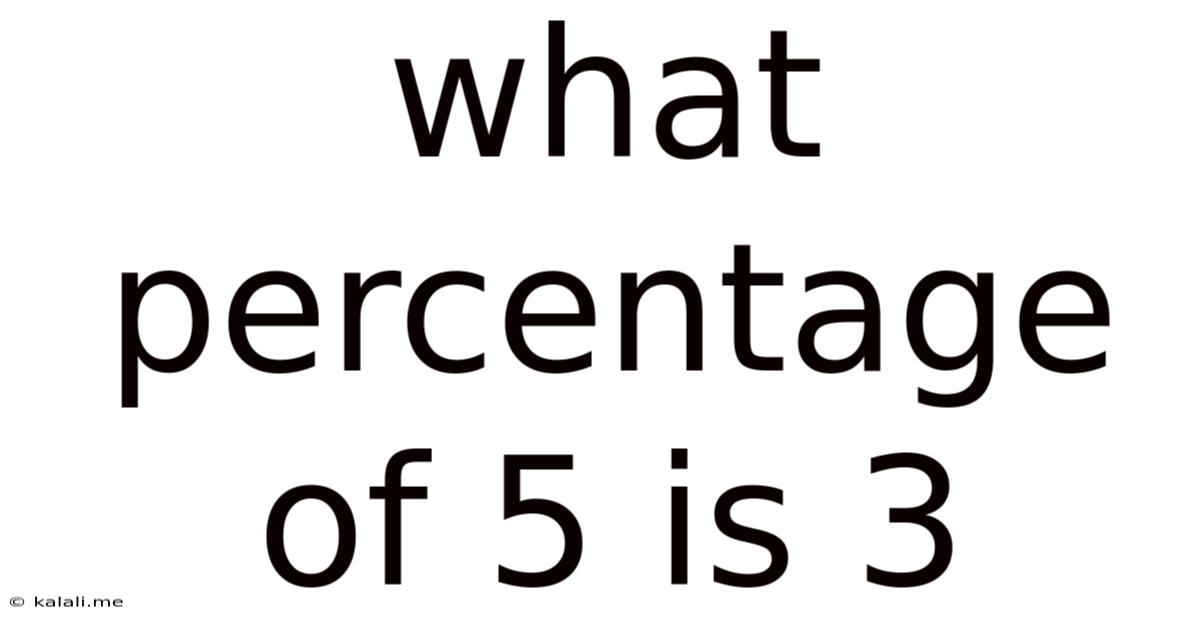
Table of Contents
What Percentage of 5 is 3? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the question, "What percentage of 5 is 3?", providing a step-by-step explanation of the calculation, exploring different approaches, and offering practical examples to solidify your understanding of percentage problems. We'll also examine the broader context of percentages and their significance.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). It's a versatile tool used to represent proportions, ratios, and changes in value. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
To calculate percentages, we use the following formula:
(Part / Whole) * 100% = Percentage
In our problem, "What percentage of 5 is 3?", we can identify:
- Part: 3 (the smaller number)
- Whole: 5 (the larger number, representing the total or whole quantity)
Calculating the Percentage: Step-by-Step
Let's apply the formula to determine what percentage of 5 is 3:
-
Divide the Part by the Whole: 3 / 5 = 0.6
-
Multiply the Result by 100%: 0.6 * 100% = 60%
Therefore, 3 is 60% of 5.
Alternative Methods for Calculating Percentages
While the formula above is the most straightforward method, alternative approaches can be equally effective, especially when dealing with more complex scenarios or when mental calculations are preferred.
Method 2: Using Proportions
We can set up a proportion to solve the problem:
3/5 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
5x = 300
x = 300 / 5
x = 60
Therefore, x = 60%, confirming our previous result.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%:
-
Convert the fraction 3/5 to a decimal: 3 ÷ 5 = 0.6
-
Multiply the decimal by 100%: 0.6 * 100% = 60%
This approach highlights the direct relationship between decimals and percentages.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in numerous real-world situations. Let's explore some examples:
1. Sales and Discounts: A store offers a discount of $2 on an item originally priced at $5. What is the percentage discount?
Using our formula: (2 / 5) * 100% = 40%. The discount is 40%.
2. Test Scores: A student scores 3 out of 5 on a quiz. What is their percentage score?
(3 / 5) * 100% = 60%. The student achieved a 60% score.
3. Financial Calculations: An investment grows from $5 to $8. What is the percentage increase?
First, calculate the increase: 8 - 5 = 3
Then, calculate the percentage increase using the original value as the whole: (3 / 5) * 100% = 60%. The investment grew by 60%.
4. Survey Results: In a survey of 5 people, 3 preferred a particular brand. What percentage of respondents preferred that brand?
(3 / 5) * 100% = 60%. 60% of respondents preferred the brand.
5. Data Analysis: If a company produces 5 units, and 3 are defective, what percentage of the production is defective?
(3 / 5) * 100% = 60%. 60% of the production is defective.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percentage of 5 is 3?" is relatively simple, percentage calculations can become more complex. Understanding the fundamental principles allows you to tackle more intricate scenarios:
1. Finding the Whole: If 60% of a number is 3, what is the number?
We can set up the equation: 0.6x = 3, where 'x' is the unknown number. Solving for x: x = 3 / 0.6 = 5.
2. Finding the Part: What is 60% of 5?
This is a straightforward multiplication: 0.6 * 5 = 3.
3. Percentage Change: Calculating the percentage increase or decrease between two numbers. The formula is:
[(New Value - Old Value) / Old Value] * 100%
4. Compound Percentages: Calculating percentages based on previous percentage changes. This involves applying multiple percentage calculations sequentially.
Mastering Percentages: Tips and Resources
Mastering percentages requires consistent practice and a solid understanding of the underlying concepts. Here are some tips to enhance your skills:
- Practice Regularly: Solve various percentage problems to build your proficiency.
- Visual Aids: Utilize diagrams and charts to visualize percentages and their relationships.
- Check Your Work: Always verify your answers using alternative methods to ensure accuracy.
- Real-World Applications: Relate percentage calculations to real-life scenarios to enhance understanding and retention.
- Online Resources: Numerous online resources, including tutorials, practice exercises, and calculators, can further aid your learning.
Conclusion
The question, "What percentage of 5 is 3?" provides a foundational example for understanding percentage calculations. We have explored various methods to solve this problem and demonstrated its relevance in a variety of practical applications. By mastering these fundamental concepts and employing diverse approaches, you can confidently tackle a wide range of percentage problems in your academic studies, professional life, and daily encounters. Remember, practice and application are key to building a strong understanding of this crucial mathematical concept. Through consistent practice and a clear understanding of the underlying principles, you can confidently navigate the world of percentages and utilize them effectively in various situations.
Latest Posts
Latest Posts
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
-
How Far Is 0 4 Miles To Walk
Jul 12, 2025
-
What Is 20 Percent Of 800 000
Jul 12, 2025
-
Words That Start With Y In Science
Jul 12, 2025
-
Prevent An Expressway Emergency By Merging Without
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 5 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.