What Percentage Of 6 Is 4
Kalali
Apr 07, 2025 · 5 min read
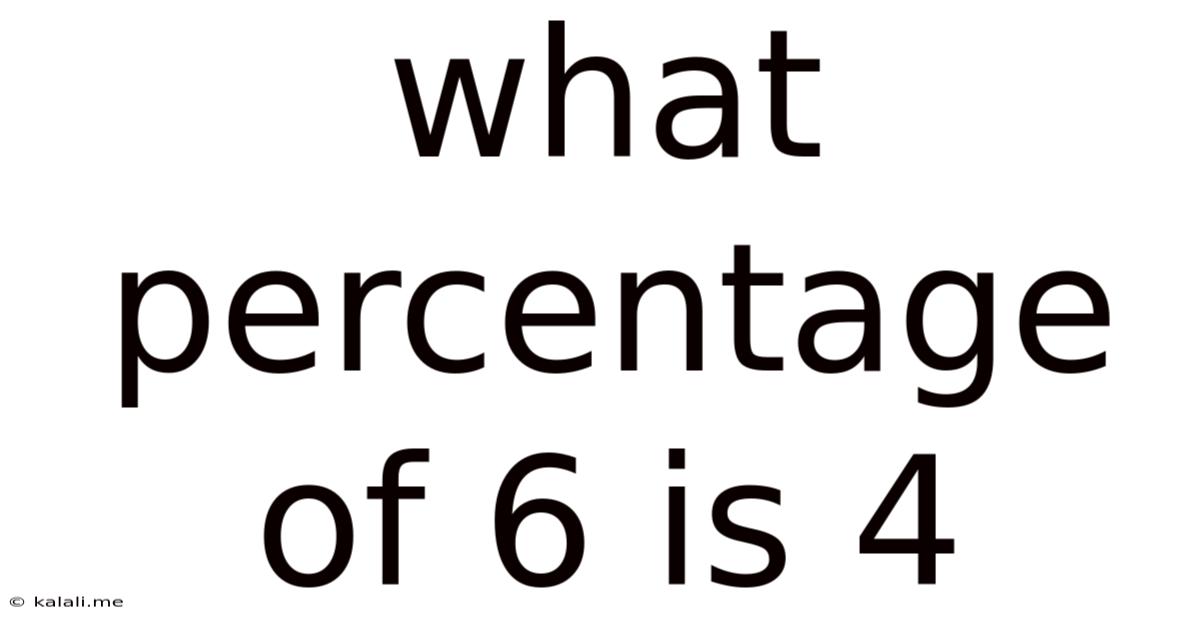
Table of Contents
What Percentage of 6 is 4? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What percentage of 6 is 4?", opens the door to a world of practical applications for percentage calculations. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will not only answer the initial question but will also delve into the underlying principles, provide multiple solution methods, and explore real-world applications.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages are a common way to represent proportions, parts of a whole, or rates of change. They are widely used because they provide a standardized and easily understandable way to compare different quantities.
Key Concepts
- Part: The portion of the whole that we are interested in. In our example, 4 is the part.
- Whole: The total amount or quantity. In our example, 6 is the whole.
- Percentage: The proportion of the part to the whole, expressed as a number out of 100. This is what we need to calculate.
Calculating "What Percentage of 6 is 4?"
There are several ways to calculate what percentage 4 represents of 6. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
(4 / 6) * 100% = Percentage
- Divide the part by the whole: 4 / 6 = 0.666666...
- Multiply the result by 100%: 0.666666... * 100% ≈ 66.67%
Therefore, 4 is approximately 66.67% of 6.
Method 2: Using Proportions
We can also solve this problem using proportions:
- Set up a proportion: x/100 = 4/6
- Cross-multiply: 6x = 400
- Solve for x: x = 400/6 ≈ 66.67
Again, we arrive at the answer: 4 is approximately 66.67% of 6.
Method 3: Using Decimal Conversion
- Divide the part by the whole: 4 / 6 = 0.666666...
- Convert the decimal to a percentage: Multiply the decimal by 100%. 0.666666... * 100% ≈ 66.67%
This method is essentially a simplified version of Method 1.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is invaluable in numerous real-world scenarios. Here are some examples:
1. Discounts and Sales
Retail stores frequently offer discounts on products. If a $60 item is discounted by 40%, you would calculate the discount as (40/100) * $60 = $24. The final price would be $60 - $24 = $36. Conversely, if you know the original price and the sale price, you can calculate the percentage discount.
2. Taxes and Interest
Calculating sales tax, income tax, or interest on loans and investments all involve percentages. For example, if the sales tax rate is 6%, and you purchase a $100 item, the tax amount would be (6/100) * $100 = $6.
3. Grade Calculations
In education, grades are often expressed as percentages. If you answered 4 out of 6 questions correctly on a test, your score would be approximately 66.67%.
4. Financial Analysis
Percentage calculations are fundamental in financial analysis. Investors use percentages to track return on investment (ROI), analyze profit margins, and assess financial ratios. For instance, a company's profit margin is calculated as (Net Profit / Revenue) * 100%.
5. Data Analysis and Statistics
Percentages are crucial for presenting and interpreting data. Charts and graphs frequently use percentages to represent proportions and trends within datasets. This allows for easy visual comparison of different categories or groups.
6. Scientific Calculations
Percentages are also used extensively in scientific fields, such as chemistry and biology, to express concentrations, yields, and error rates.
7. Everyday Life
Beyond formal applications, percentages are encountered daily. Tips in restaurants, survey results, and weather forecasts often utilize percentages to convey information concisely and effectively.
Expanding on Percentage Calculations: Further Exploration
The basic principles of percentage calculations can be expanded upon to handle more complex scenarios:
1. Calculating the Whole
If you know the percentage and the part, you can calculate the whole. For example, if 20% of a number is 10, you can set up the equation: (20/100) * x = 10. Solving for x will give you the whole number (50).
2. Calculating the Part
If you know the percentage and the whole, you can calculate the part. For instance, if you want to find 30% of 200, you calculate (30/100) * 200 = 60.
3. Percentage Change
Calculating percentage change is useful for comparing values over time. The formula is: [(New Value - Old Value) / Old Value] * 100%. A positive result indicates an increase, while a negative result indicates a decrease.
4. Compound Interest
Compound interest calculations involve repeated percentage additions. The formula takes into account the principal amount, interest rate, and the number of compounding periods. This is a crucial concept in finance and investments.
Conclusion: Mastering Percentages for Success
Mastering percentage calculations is a valuable skill with wide-ranging applications. From everyday purchases to complex financial analyses, understanding how to work with percentages empowers you to make informed decisions, interpret data effectively, and navigate various aspects of life with confidence. This comprehensive guide has provided a solid foundation, offering multiple solution methods and highlighting the real-world relevance of percentage calculations. By practicing these methods and exploring the further applications mentioned, you can significantly enhance your numerical literacy and problem-solving abilities. Remember, the seemingly simple question, "What percentage of 6 is 4?", serves as a springboard to a vast and practical understanding of percentages.
Latest Posts
Latest Posts
-
What Is 9 10 As A Decimal
Apr 09, 2025
-
How Many Grams In A Kilo Of Gold
Apr 09, 2025
-
How Much Is 42 Cm In Inches
Apr 09, 2025
-
Which Ocean Is Colder Atlantic Or Pacific
Apr 09, 2025
-
How Many Inches Are In 4 5 Feet
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 6 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.