What Percentage Of 60 Is 10
Kalali
Mar 21, 2025 · 5 min read
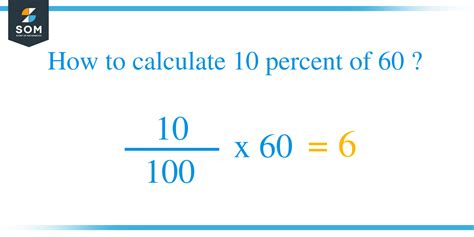
Table of Contents
What Percentage of 60 is 10? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percentage of 60 is 10?" – opens the door to a broader understanding of percentages, their applications, and how to solve similar problems with confidence. This article will not only answer the question directly but also explore the underlying mathematical principles, offer multiple solution methods, and delve into real-world examples where percentage calculations are crucial.
Understanding Percentages: The Foundation
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10.
This fundamental concept allows us to convert percentages to decimals and fractions, and vice-versa. For instance:
- 25% = 25/100 = 0.25
- 0.75 = 75/100 = 75%
- 1/4 = 25/100 = 25%
This flexibility is key to solving percentage problems efficiently.
Method 1: The Proportion Method
The proportion method is a classic and intuitive way to solve percentage problems. It leverages the fact that percentages represent a ratio. We can set up a proportion to find the unknown percentage:
Part / Whole = Percentage / 100
In our case:
- Part: 10
- Whole: 60
- Percentage: x (this is what we need to find)
Substituting these values into the proportion equation, we get:
10 / 60 = x / 100
Now, we solve for x:
- Cross-multiply: 10 * 100 = 60 * x
- Simplify: 1000 = 60x
- Solve for x: x = 1000 / 60 = 16.666...
Therefore, 10 is approximately 16.67% of 60.
Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then using multiplication. We can express the problem as:
Percentage = (Part / Whole) * 100
Let's apply this to our problem:
- Divide the part by the whole: 10 / 60 = 0.16666...
- Multiply by 100 to convert to a percentage: 0.16666... * 100 = 16.666...%
Again, we arrive at approximately 16.67%.
Method 3: Using a Calculator
Modern calculators often have a percentage function that simplifies the calculation. Simply enter 10, divide by 60, and then multiply by 100. The calculator will directly display the percentage.
Real-World Applications: Where Percentages Matter
Percentage calculations are ubiquitous in everyday life. Here are a few examples:
- Sales and Discounts: A common use is calculating discounts in stores. A "20% off" sale means you pay 80% of the original price.
- Taxes and Interest: Calculating sales tax, income tax, and interest on loans or savings accounts all rely heavily on percentage calculations.
- Statistics and Data Analysis: Percentages are fundamental to representing data and drawing conclusions from surveys, polls, and scientific studies. Think about employment rates, population growth, or the success rate of a medical treatment.
- Finance and Investments: Understanding returns on investment, profit margins, and financial ratios all require a strong grasp of percentage calculations. Percentage change is crucial for tracking stock performance or the value of assets.
- Grades and Test Scores: Academic performance is often expressed as percentages, helping students and teachers track progress and identify areas for improvement.
- Cooking and Baking: Recipes frequently use percentages, particularly in baking, where precise ratios are essential for successful outcomes. For example, bread recipes may specify a certain percentage of hydration (water to flour ratio).
- Sports Statistics: Many sports statistics use percentages, such as batting averages in baseball, free throw percentages in basketball, and completion percentages in football. Understanding these percentages is key for analyzing player performance and team strategy.
- Surveys and Polls: Results of surveys and polls are frequently presented using percentages to represent the proportion of respondents who chose a particular option. This allows for easy comparison and visualization of responses.
Expanding the Concept: Percentage Increase and Decrease
Often, we're interested in not just the percentage one number represents of another but also the percentage change between two numbers. For example, we might want to know the percentage increase in sales from one year to the next, or the percentage decrease in unemployment. The formula for percentage change is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
A positive result indicates an increase, while a negative result indicates a decrease.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percentage of 60 is 10?" is relatively straightforward, the principles behind it apply to more complex scenarios. For example:
- Finding the whole: If you know a percentage and the part, you can use the same principles to find the whole.
- Finding the part: If you know a percentage and the whole, you can find the part.
- Multiple percentage changes: Calculating the effect of multiple consecutive percentage increases or decreases requires a slightly more nuanced approach, involving careful multiplication of the decimal equivalents.
Mastering the fundamental principles of percentages unlocks the ability to solve a vast range of problems across numerous disciplines. By understanding the underlying mathematics and practicing different solution methods, you can build your confidence and competence in this essential area of numeracy.
Conclusion: The Power of Percentages
The answer to "What percentage of 60 is 10?" is approximately 16.67%. However, the true value of this seemingly simple question lies in its ability to illuminate the broader world of percentage calculations. Understanding percentages is not just about solving math problems; it's about understanding and interpreting data, making informed decisions, and navigating the complexities of the modern world. From shopping and investing to analyzing statistics and understanding scientific research, a solid grasp of percentages is an invaluable skill. By mastering the techniques outlined here, you can confidently tackle a wide array of percentage-related problems and unlock a deeper understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Least Common Multiple Of 2 And 7
Mar 28, 2025
-
How Many Litres In 7 Gallons
Mar 28, 2025
-
Ar Kr And Xe Reactive Or Not Reactive
Mar 28, 2025
-
How Many Grams In 300 Milligrams
Mar 28, 2025
-
How Much Is 20 Ounces Of Water
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 60 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
