What Percentage Of 80 Is 10
Kalali
Apr 27, 2025 · 5 min read
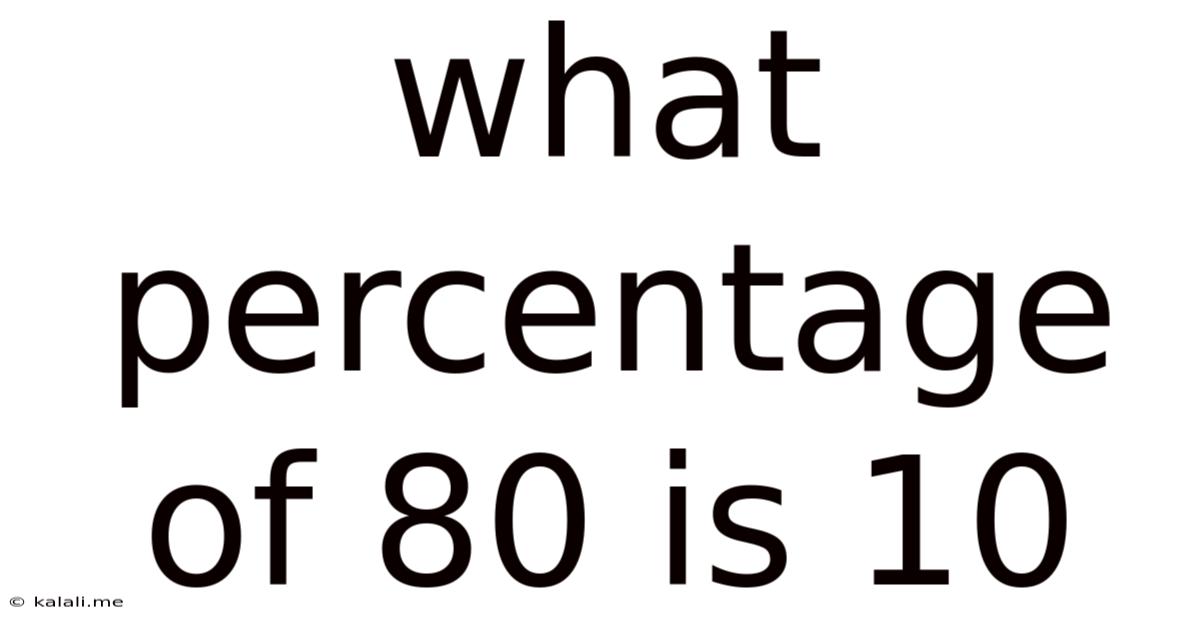
Table of Contents
What Percentage of 80 is 10? A Deep Dive into Percentage Calculations and Applications
This seemingly simple question, "What percentage of 80 is 10?", opens the door to a surprisingly vast world of mathematical concepts and practical applications. While the answer itself is straightforward, understanding the underlying principles and methods involved is crucial for anyone looking to improve their mathematical literacy and problem-solving skills. This article will not only answer the question directly but also explore the various ways to calculate percentages, delve into the significance of percentages in different fields, and provide practical examples to solidify your understanding.
Meta Description: Discover how to calculate percentages with a detailed explanation of how to determine what percentage of 80 is 10. This guide covers various methods, real-world applications, and practical examples.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are used to express proportions, rates, and changes in a way that is easily understood and compared. They are ubiquitous in everyday life, appearing in discounts, interest rates, tax calculations, statistics, and much more.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Calculating "What Percentage of 80 is 10?"
Now, let's apply this formula to answer our main question: What percentage of 80 is 10?
In this case:
- Part: 10
- Whole: 80
Plugging these values into the formula, we get:
(10 / 80) * 100 = 12.5%
Therefore, 10 is 12.5% of 80.
Alternative Methods for Calculating Percentages
While the above method is the most straightforward, there are other approaches you can use to calculate percentages, depending on the complexity of the problem and your personal preference.
Method 2: Using Proportions:
You can set up a proportion to solve the problem. A proportion is an equation that states that two ratios are equal. In this case, we can set up the proportion:
10/80 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we can cross-multiply:
80x = 1000
x = 1000/80
x = 12.5
Therefore, x = 12.5%, confirming our previous result.
Method 3: Using Decimal Equivalents:
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. For example, 12.5% is equal to 0.125. We can use this to solve our problem:
0.125 * 80 = 10
This confirms that 12.5% of 80 is indeed 10.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in a wide range of real-world situations. Here are just a few examples:
-
Retail Sales and Discounts: Stores frequently advertise discounts as percentages. For example, a "20% off" sale means that the price is reduced by 20% of the original price. Calculating the final price after a discount requires understanding how to find a percentage of a number.
-
Finance and Investments: Interest rates on loans and savings accounts are expressed as percentages. Understanding percentage calculations is crucial for managing personal finances and making informed investment decisions. Calculating compound interest involves repeated percentage calculations.
-
Taxes and Tax Rates: Taxes are often expressed as percentages of income or the value of goods and services. Calculating taxes and understanding tax brackets requires a thorough understanding of percentage calculations.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions and changes in data. For example, survey results are often presented as percentages to make the data more accessible and easier to interpret. Understanding percentage change calculations is vital for analyzing trends and making data-driven decisions.
-
Scientific Research: Percentages are crucial in many scientific fields, such as expressing the concentration of a solution, the percentage of a certain element in a compound, or the success rate of an experiment.
-
Everyday Life: Calculating tips at restaurants, figuring out the percentage of a raise, determining the sale price of an item, or understanding nutritional information on food labels all involve the application of percentage calculations.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond simply finding what percentage one number is of another, understanding percentage increase and decrease is equally important.
Percentage Increase: This is calculated by finding the difference between the new value and the original value, dividing the difference by the original value, and multiplying by 100.
Formula: [(New Value - Original Value) / Original Value] * 100
Example: If the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100 = 20%
Percentage Decrease: This is calculated similarly, but the difference is subtracted from the original value.
Formula: [(Original Value - New Value) / Original Value] * 100
Example: If the price of an item decreases from $60 to $50, the percentage decrease is:
[(60 - 50) / 60] * 100 = 16.67%
Troubleshooting Common Percentage Calculation Errors
Even simple percentage calculations can lead to errors if not approached carefully. Here are some common pitfalls to avoid:
-
Incorrect Formula Application: Ensure you're using the correct formula for the specific type of percentage calculation you're performing.
-
Order of Operations: Follow the order of operations (PEMDAS/BODMAS) correctly when performing calculations involving multiple operations.
-
Decimal Errors: Be mindful of decimal points when converting percentages to decimals and vice versa.
-
Rounding Errors: Be aware of rounding errors, especially when dealing with multiple steps in a calculation. Round only at the final step for the most accurate result.
Conclusion: Mastering Percentages for Success
The seemingly simple question of "What percentage of 80 is 10?" serves as a springboard to a comprehensive understanding of percentage calculations and their widespread applications. From everyday transactions to complex financial analyses and scientific research, the ability to accurately and efficiently calculate percentages is a valuable skill. By understanding the fundamental principles, exploring different calculation methods, and practicing with real-world examples, you can master percentages and enhance your mathematical proficiency in various aspects of your life. Remember to always double-check your work and be mindful of potential errors to ensure accuracy. The ability to confidently work with percentages will undoubtedly empower you to make better informed decisions across many fields.
Latest Posts
Latest Posts
-
What Percent Is 5 Out Of 8
Apr 27, 2025
-
How Many Cups Are In 12 Ounces
Apr 27, 2025
-
How Many Grams Are In 0 50 Kilograms
Apr 27, 2025
-
Convert 94 Degrees Fahrenheit To Celsius
Apr 27, 2025
-
How Much Is 500 Minutes In Hours
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 80 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.