What Times What Times What Equals 54
Kalali
Jul 03, 2025 · 5 min read
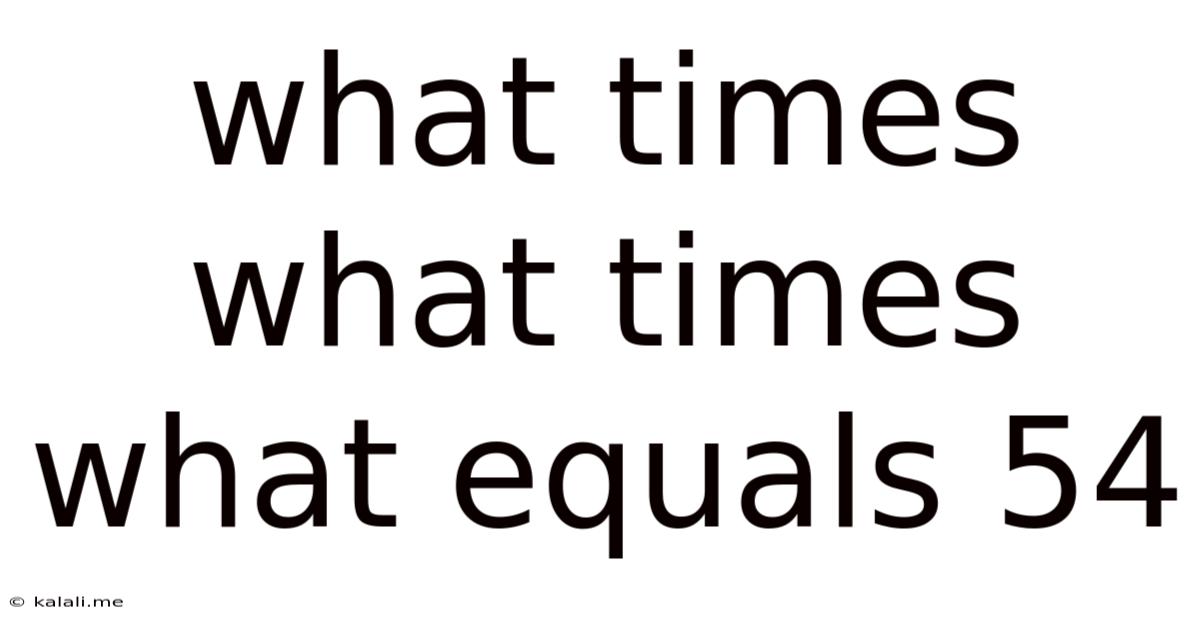
Table of Contents
What Times What Times What Equals 54? Exploring the Mathematical Possibilities and Problem-Solving Strategies
This seemingly simple question, "What times what times what equals 54?", opens a door to a fascinating exploration of number theory, factorization, and problem-solving strategies. At first glance, it might appear straightforward, but delving deeper reveals multiple solutions and valuable insights into mathematical thinking. This article will delve into various approaches to finding the answer, discuss the concept of prime factorization, and explore broader implications for mathematical reasoning. We'll also touch upon how to approach similar problems and the importance of methodical problem-solving.
Understanding the Problem: Finding the Factors of 54
The core of the problem lies in finding three numbers that, when multiplied together, result in 54. This requires understanding the concept of factors—numbers that divide evenly into another number without leaving a remainder. To find the solution, we need to identify the factors of 54. A good starting point is prime factorization.
Prime Factorization: The Building Blocks of Numbers
Prime factorization is the process of breaking down a number into its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization provides a unique and fundamental representation of any number.
Let's find the prime factorization of 54:
- We can start by dividing 54 by 2: 54 ÷ 2 = 27.
- 27 is not divisible by 2, but it is divisible by 3: 27 ÷ 3 = 9.
- 9 is also divisible by 3: 9 ÷ 3 = 3.
- Finally, 3 is a prime number.
Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3, or 2 x 3³.
Finding the Solutions: Combining Prime Factors
Now that we have the prime factorization, we can explore different combinations of three numbers that multiply to 54. We can regroup the prime factors in various ways:
-
Solution 1: Using Prime Factors Directly: We can use the prime factors directly: 2 x 3 x 9 = 54. This is a straightforward solution derived from the prime factorization.
-
Solution 2: Exploring Other Factor Combinations: We can also explore other factor combinations. For example, we know that 6 x 9 = 54, and we can express 6 as 2 x 3. Therefore another solution is 2 x 3 x 9. Notice this is the same as Solution 1.
-
Solution 3: Including Negative Numbers: Since a negative number multiplied by a negative number results in a positive number, we can also consider negative factors. For example: (-2) x (-3) x 9 = 54, (-2) x 3 x (-9) = 54, and many other combinations involving negative numbers.
-
Solution 4: Fractions and Decimals: The question doesn't explicitly restrict us to whole numbers. We could use fractions and decimals. For instance, 1 x 6 x 9 = 54. We can break this down further: 1 x 2 x 27, or many more combinations. This opens up an infinite number of solutions if we consider fractions and decimals.
Beyond Whole Numbers: Infinite Possibilities
If we expand the possibilities to include fractions and decimals, the number of solutions becomes infinite. For example:
- 1 x 1 x 54
- 1 x 2 x 27
- 1 x 3 x 18
- 1 x 6 x 9
- 2 x 3 x 9
- ...and so on.
Each of these sets of three numbers satisfies the condition, showcasing the richness and complexity of even seemingly simple mathematical problems. This demonstrates the importance of clarifying the constraints of the problem (e.g., are we limited to whole numbers, integers, or can we include fractions and decimals?).
Problem-Solving Strategies: A Systematic Approach
Solving mathematical problems effectively requires a systematic approach. Here's a breakdown of a useful strategy:
-
Understanding the Problem: Clearly define what the problem is asking. In this case, we need to find three numbers whose product is 54.
-
Identifying Key Concepts: Recognize relevant mathematical concepts. Here, the concepts of factors, prime factorization, and multiplication are crucial.
-
Developing a Plan: Outline the steps you'll take to solve the problem. In this case, prime factorization is a helpful starting point.
-
Executing the Plan: Systematically apply your chosen method (prime factorization in this case).
-
Checking Your Work: Verify your solutions by multiplying the three numbers to ensure their product equals 54.
Expanding the Problem: Variations and Extensions
This problem can be extended in numerous ways:
-
Different Target Numbers: Try finding three numbers that multiply to different target numbers (e.g., 72, 100, 1000). This reinforces the practice of prime factorization and factor identification.
-
More Than Three Numbers: Explore finding four, five, or more numbers that multiply to a given target. This adds another layer of complexity.
-
Adding Constraints: Introduce constraints, such as limiting the numbers to odd numbers, even numbers, or numbers within a specific range.
Conclusion: The Value of Exploration
The simple question "What times what times what equals 54?" unveils a surprisingly rich landscape of mathematical exploration. From prime factorization to the infinite possibilities when including fractions and decimals, this problem highlights the importance of understanding fundamental mathematical concepts and employing systematic problem-solving techniques. By exploring variations and extensions of this problem, we can strengthen our mathematical skills and appreciate the beauty and complexity hidden within seemingly simple mathematical questions. The key takeaway is the iterative process of exploring solutions and understanding the diverse mathematical concepts involved, ultimately leading to a deeper appreciation for the subject.
Latest Posts
Latest Posts
-
John Deere Oil Filter Am125424 Cross Reference Chart
Jul 31, 2025
-
How Is Grendel Characterized In This Excerpt
Jul 31, 2025
-
I Was Born In 1971 How Old Am I
Jul 31, 2025
-
Which Statement Best Illustrates An Example Of Economic Specialization
Jul 31, 2025
-
Is 6 Inches Of Rain A Lot
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about What Times What Times What Equals 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.