What Times What Times What Equals 60
Kalali
Jul 23, 2025 · 5 min read
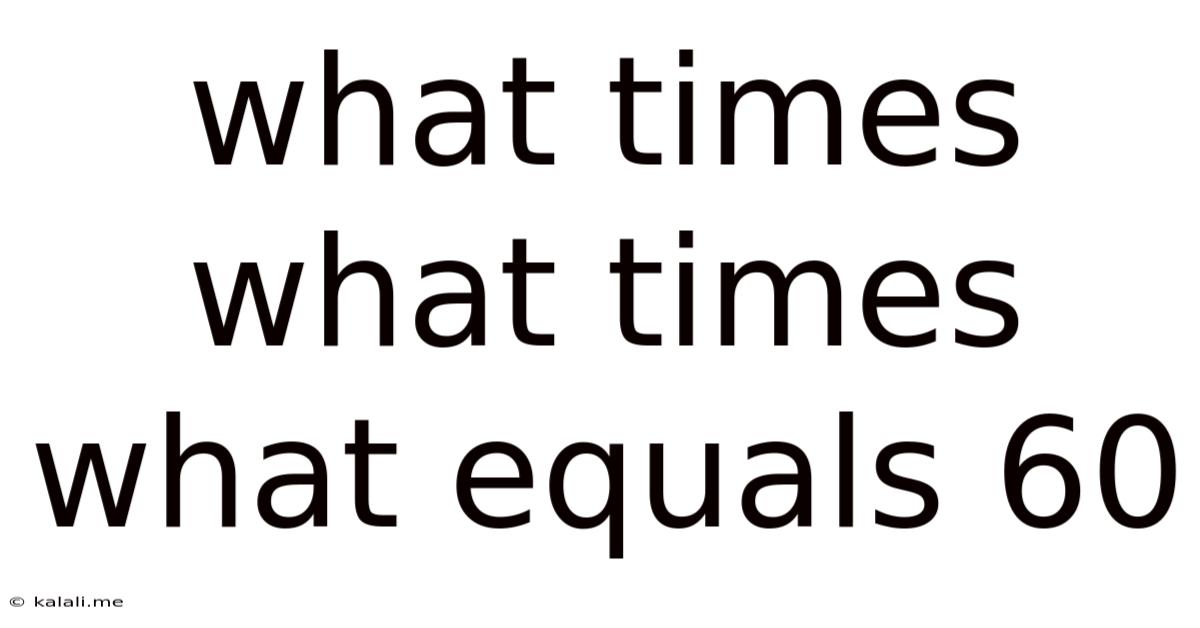
Table of Contents
What Times What Times What Equals 60? Exploring the Mathematical Possibilities and Problem-Solving Strategies
Finding three numbers that multiply to equal 60 might seem like a simple math problem, but it opens the door to a fascinating exploration of factors, multiples, and problem-solving strategies. This isn't just about finding a solution; it's about understanding the breadth of possibilities and developing a systematic approach to tackle similar problems. This article delves deep into this seemingly simple equation, unveiling various solutions, exploring mathematical concepts, and providing practical strategies for approaching similar challenges.
Understanding the Problem: Factorization and Multiples
The core of this problem lies in understanding the concept of factorization. Factorization is the process of breaking down a number into smaller numbers that, when multiplied together, produce the original number. In our case, we're looking for three factors of 60. Conversely, we could also view this through the lens of multiples: 60 is a multiple of what three numbers? Both perspectives lead to the same solution, but offer different starting points for our investigation.
Finding the Obvious Solutions: Starting with Whole Numbers
Let's start with the most straightforward approach: using whole numbers. We can begin by listing the factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. From this list, we can easily identify several sets of three numbers that multiply to 60:
- 1 x 1 x 60: This is a trivial solution, but it's valid nonetheless.
- 1 x 2 x 30: A slightly more interesting combination.
- 1 x 3 x 20: Demonstrates the various permutations possible.
- 1 x 4 x 15: Continuing to explore different factor combinations.
- 1 x 5 x 12: We're systematically working through the factors.
- 1 x 6 x 10: Notice how changing one factor significantly alters the others.
- 2 x 2 x 15: Introducing repeated factors.
- 2 x 3 x 10: Another combination with different factors.
- 2 x 5 x 6: A balanced combination of factors.
- 3 x 4 x 5: A commonly encountered solution due to its relatively small numbers.
Expanding the Possibilities: Including Negative Numbers and Fractions
Our initial exploration focused on positive whole numbers, but the problem doesn't restrict us to this set. Let's consider the possibilities when negative numbers are included. Since a negative number multiplied by a negative number results in a positive number, we can introduce negative factors:
- (-1) x (-1) x 60: This is a valid solution because (-1) * (-1) = 1.
- (-1) x 2 x (-30): Notice how the negative signs can be distributed amongst the factors.
- (-1) x (-2) x 30: Many more combinations become available with negative numbers.
Furthermore, we can broaden our horizons by considering fractional numbers. The possibilities become virtually limitless here. For example:
- 2 x 3 x 10: We can rewrite this as: (2/x) x (3x) x 10, where 'x' can be any non-zero number. This illustrates how infinitely many solutions exist if we allow for fractional numbers.
A Systematic Approach: Prime Factorization and Tree Diagrams
To systematically explore all possible whole number solutions, we can utilize prime factorization. Prime factorization involves breaking down a number into its prime factors – numbers only divisible by 1 and themselves. The prime factorization of 60 is 2 x 2 x 3 x 5.
Using this prime factorization, we can build up our three-factor combinations. For instance:
- (2 x 2) x 3 x 5 = 60
- 2 x (2 x 3) x 5 = 60
- 2 x 2 x (3 x 5) = 60
- (2 x 5) x 2 x 3 = 60
- ...and so on.
A tree diagram can be a helpful visual aid to explore these combinations systematically. Start with 60, then branch out to its factors, and continue branching until you reach the prime factors. Then, work backwards to recombine the prime factors into sets of three.
Beyond the Numbers: Problem-Solving and Mathematical Thinking
This seemingly simple problem showcases fundamental mathematical concepts and cultivates valuable problem-solving skills. It teaches us to:
- Think systematically: Develop a structured approach to explore all possible solutions.
- Consider different perspectives: Approach the problem through the lens of factors and multiples.
- Embrace the limitations and expansions: Understand the impact of restricting ourselves to whole numbers versus expanding to include negatives and fractions.
- Utilize visual aids: Emphasize the role of tree diagrams or other methods to visualize the process.
Applications and Extensions: Real-World Connections and Further Exploration
Understanding factorization and multiples has broad applications in various fields, including:
- Computer science: In cryptography and algorithm design.
- Engineering: In calculations related to structural design and optimization.
- Finance: In calculating compound interest and investment strategies.
This problem can also be extended in many ways:
- What times what times what times what equals 60? This increases the complexity and number of solutions.
- Find three consecutive numbers that multiply to a specific value. This adds a constraint to the problem.
- Explore similar problems with different target numbers. Generalize the problem-solving strategy.
By exploring this seemingly simple equation, "what times what times what equals 60?", we've unearthed a rich mathematical landscape that goes beyond finding solutions. It's a journey of exploration, highlighting the power of systematic thinking, the beauty of factorization, and the endless possibilities within seemingly simple mathematical problems. The true value lies not just in the answers themselves but in the process of discovering them.
Latest Posts
Latest Posts
-
Can A Felon Hunt With A Crossbow
Jul 23, 2025
-
11 Out Of 14 Is What Percent
Jul 23, 2025
-
Best Friend Song From Rob And Big
Jul 23, 2025
-
How Many Chicken Tenderloins In A Pound
Jul 23, 2025
-
What Is The Gcf Of 36 And 42
Jul 23, 2025
Related Post
Thank you for visiting our website which covers about What Times What Times What Equals 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.